A main goal of reformed physics teaching is the development of deep conceptual understanding within a robust interconnected framework. New ideas should not only “make sense”; they should be well connected to prior concepts and ideas. This is the antidote to rote algorithmic learning and disjointed knowledge. (I always say, “A little compartmentalized learning is a dangerous thing!”) This goal can be realized through the careful exploration of the two aspects of circular motion: force and acceleration - cause and effect.

There are two persistent ideas that many students have regarding uniform circular motion: (1) that there must be a forward (tangential) force that keeps the object moving in a circle; and (2) there must be an outwards force keeping it from falling inwards. These ideas can very happily coexist in the fertile student mind along with the teacher-approved notion of a radially inward net force. For novice physics students all three possibilities may seem plausible and may not seem mutually exclusive. Only after repeated and explicit examination, followed up by careful reinforcement long after the circular motion unit is finished, will the misconceptions wither away.

The appeal of a forwards force can stem from insecurity with Newton’s 1st law in the context of two-dimensional motion. The idea that an external force is not required for an object to maintain a constant speed is strange enough. To compound things, physics suffers from very rich laws whose many consequences are not well unpacked for students. Mathematicians have theorems and their theorems’ offspring: lemmas. We need these for physics! For example, Newton’s 2nd Law should have a lemma, which I affectionately call the Orthogonality Principle, stating that “a net force in one direction does not affect the speed in a perpendicular direction.” Obvious, right? Not for most students. This is a fundamental feature of the 2nd law that lies at the heart of understanding circular motion. Its earlier introduction when studying projectile motion can greatly help dispel the “forwards force” notion. Another useful lemma students should develop while exploring circular motion is “a force parallel to an object’s direction of motion only changes its speed; a force perpendicular to its motion only changes its direction.” Both lemmas are helpful ways of capturing the nuances of Newton’s laws applied to two-dimensional motion.

The allure of an outwards force in circular motion is very great and surprisingly persistent (even amongst a number of teachers I have workshopped). We only have ourselves to blame for this, and by “ourselves” I mean our physical selves: when we travel in a circle we feel an outwards effect of some kind. It takes careful work to reinterpret this valuable observation. This work is a process that should begin long before the topic of circular motion is reached. The physical sensation of acceleration needs to be made sense of early on in the context of linear acceleration. The goal is the understanding that when accelerating due to any force other than gravity, our physical sensation is that of being pushed in a direction opposite to our acceleration. For example, we feel pressed into the seat of a car that is speeding up. This provides students with a familiar tool to help understand the sensation of being pushed outwards without having to conjure up an outwards force.

Especially in the case of an object being whirled on a string, another rationale students often invoke for the existence of an outwards force is the need to prevent the object from traveling directly inwards to the centre of the circular path. Another still is their attempt to explain why there is any tension in the string at all! These proposals need to be met with a careful kinematic exploration of circular motion. I find this is easiest in the context of orbits and the recognition of the need for orbital speed. Another valuable example is a rollercoaster loop with an unattached car upside- down at the top. The car could in fact fall straight down, but with a suitable tangential speed, it moves far enough forward while it “falls” that it remains in contact with the track.

A telling example of the challenges of understanding circular motion comes from a study by Sue Allen and Frederick Reif in which the researchers pose to a group of students and physics professors from UC Berkeley a simple question: What is the direction of the acceleration of a pendulum bob as it speeds up and reaches point C in the diagram to the right? Only 3 out of 5 of the veteran professors answered correctly, even when prompted to clarify their responses. Indeed, the matter of forces in circular motion can be very thorny. (What is the correct answer?)

One of the great things about physics is that a small number of ideas have the power to explain so many different things. Physicists toil to reduce the number of necessary ideas. It’s kind of an obsession. Teachers do a bad, bad thing when we needlessly increase that number. This brings me to a dirty trick we pull on our students. By this point in their studies, students already have a name for the idea “the combined effect of all the forces in one direction” – known as the net force in, let’s say, the radial direction. But then when circular motion comes along, we introduce this new thing “Fc” and our attempts at building a deep, robust understanding of circular motion lurches to a halt.



I am quite pleased to note that in Randall Knight’s new textbook, which is deeply infused with physics education research, the mischievous Fc never appears. There are a number of very good reasons for never using this symbol or introducing an equation like Fc = mv2/r. The main reason is that there is a perfectly good idea, F_net = ma, which really has this circular motion business well covered. Besides, you would never introduce a “handy” equation like Fnet = m(v2-v1)/Δt, owing to your confidence in your students’ ability to find a strategy to determine the acceleration. So why sell them short with circular motion? If students don’t begin their thinking about circular motion with F_net = ma they are not making vital reinforcements between prior understanding and this challenging new topic. It is crucial that students learn that there are no new laws for circular motion. Even if you introduce the centripetal force equation as a convenient short cut, students will memorize it, and in doing so will cut short their thinking (which is bad).



The Physics Union Mathematics program developed by Eugenia Etkina and Alan van Heuvelen at Rutgers University does a great job of emphasizing the deep connection between the kinematic and dynamic pictures of circular motion. If you email Professor Etkina you may receive a password to the website which has an astounding set of PER informed physics units. My own treatment of circular motion draws heavily upon their work. They take great pains to highlight how a velocity vector analysis of circular motion (acceleration points to the centre) agrees with a force diagram analysis (net force points to the centre) courtesy of, you guessed it, Newton’s second law. These are not obvious results to be glossed over; they are pillars of a deeper understanding.

I have other concerns with the gormless F_c. Textbook authors don’t really seem to use it and its namesake, the “centripetal force”, honestly. The adjective “centripetal” is a valuable label when describing a familiar force that has a component responsible for keeping an object moving in a circle (my definition). For example: “When Mitt Romney makes a 180° turn in policy, political expediency is the centripetal force”. Traditional texts define the centripetal force as F_c ≡ F_net, which is a problem for non-uniform circular motion. But even if we understand that they really mean the radial component of the net force, authors seldom use it this way in their descriptions; they tend to describe single, inward forces as the centripetal force. Furthermore, this term and its notation seem to be no more than an affectation of high school and introductory physics texts. In more advanced studies the term is abandoned and central forces are described or angular motion and moments are used.

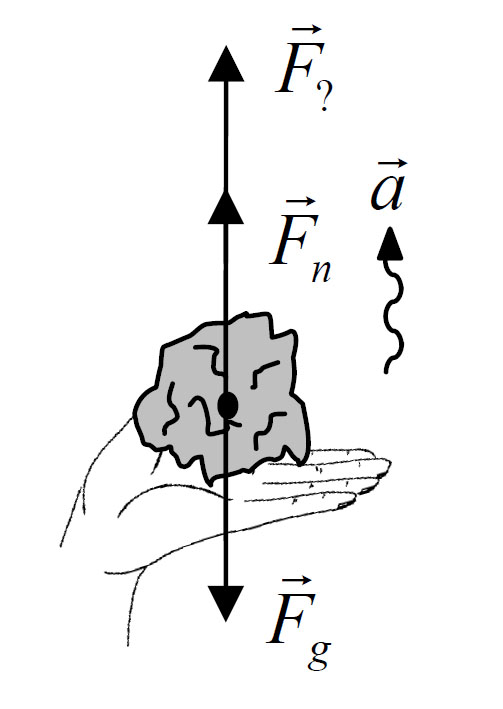
Unfortunately, students are often quite relieved when you provide them with a new force, F_c. Perhaps it provides a convenient scapegoat on which to blame the mystery of circular motion. Just as novice physics students will often invent a mysterious new force to explain the upward acceleration of a held object (see the FBD above), they are happy to have a brand new force to explain the peculiarities of circular motion. Perhaps you have noticed how F_c tends to appear in free-body diagrams in curious locations or in the place of other, reasonable forces. They will stop thinking carefully about how friction might be keeping the car going around the corner. Why should they: it’s the F_c that’s responsible! Other times the F_c appearing in their FBDs corresponds to no known physical interaction. But what can we expect: neither does their physical experience of circular motion! (The outward force, that is.)

Learning to represent the physics of a situation in a wide variety of ways is another key to developing a robust, well-connected understanding. Those in the know call this “multiple representations”. Depending on the topic, there are a variety of possible representations. Shown below is an example for circular motion. A great exercise is to provide one or two of these representations and have students devise the others. This often involves quite a bit of good old know-how and also some amusing creativity!

All of the ideas discussed here can be used with any mode of classroom teaching: old-fashioned lecture or new-fangled group work (my modus operandi). But to be sure, your students will get more out of their experience the more they explain their own ideas to one another. I teach circular motion over five (yes, five!) classes using a variety of investigations and activities. Don’t mess around: if you’re going to do it, do it well. Follow this link to my website where you can explore my circular motion lessons and syllabus, amongst the other materials for my course. Finally, I re- issue my standing invitation: the door to my classroom is always open. Just email me if you would like to drop by and see a lecture-free, reformed physics class in action.

• Use the terms radial and tangential whenever possible (a_r = v²/r, F_net t = 0)
  

• Only use the term “centripetal” as an adjective for familiar inward forces

• Always start problems with F_net = ma; banish F_c
  

• Reinforce agreement between the kinematic picture and force picture
  

• Use multiple representations
  

• Provide activities that motivate the presence of an inward net force and that help refute the existence of forward or outward forces

• Help students explain why the object doesn’t travel towards the centre of the circle and why we feel an outward force
  

• Create a lemma. Name it after yourself! “Parallel forces change speed. Perpendicular forces change direction.”
  

• Make sure students’ understanding will generalize easily to non-uniform circular motion