Forces are the bread-and-butter of physics teaching (mmm… butter). Most of us spend a good chunk of grades 11 and 12 teaching Newton’s Laws and their applications. We regard Newton as a starting point for a healthy understanding of how our universe operates. But what if there is a deeper idea, one that force emerges from and that subsumes it? There are alternate interpretations of Newtonian mechanics (e.g. Lagrangians, Hamiltonians, thespians) that dispense with the idea of force and hint at something more fundamental. An important part of this deeper level of physics is the idea of an interaction. Two particles may interact with each other and exchange fundamental physical quantities such as momentum and energy. This idea may easily be expanded to include quantum mechanics where quanta of the fields interact and exchange other quantities like charge, spin, and lepton number. Interactions can be thought of as the basic units of change, and therefore causality in our universe, and they arise in just four types: strong, weak, electromagnetic and gravitational. We usually call these fundamental interactions “forces”, but they do much more than just change the velocity of a particle.

For now we will put aside the quantum world and examine a classical model of an interaction. In this idealized world-view, we can imagine two particles colliding. The mechanism of the collision (normal forces → electromagnetic interactions → virtual photon exchange → loop quantum gravity?) is not our focus here. We are simply interested in comparing what we know about the particles before and after the interaction. Due to the collision interaction, the velocity of each particle has changed. If we were to watch one of the particles we would say that it behaved as if it were pushed or pulled somehow. The results of the interaction correspond to our intuitive everyday notion of force, but we should be cautious. When we use the word force, we really mean: “that aspect of an interaction that causes the velocity of a particle to change”. The interaction also caused energy and momentum to be transferred. If we go looking for this force, it dissolves away as we go deeper into the mechanisms, but the energy and momentum transfer are still there. The term “force” is just shorthand for a part of an interaction. If we were especially observant we might notice that the other particle in our interaction also changed its velocity, meaning it experienced a force as well. In classical mechanics without fields, we notice that interactions always give rise to a pair of forces with a remarkable set of properties, hinting at the reciprocal nature of an interaction.

None of what I describe above is breaking news but it does lead us to a powerful pedagogical strategy: from the beginning, teach students to think first about the interactions between objects, reinforcing our understanding that an interaction is a two-way street. Then you can teach them how to shift their focus from one object to the other and examine the parts of the interaction that we are interested in — the forces. Approaching forces in this way marks a deep conceptual and pedagogical shift with the purpose of packaging in one idea — the interaction — an array of force concepts that usually remain disconnected in students’ minds. Furthermore, the “distinct” topics of force and energy become much more firmly linked when students realize that they both involve the tracking of interesting quantities during the same interactions. One of the guiding principles of physics education research (PER) is that it is worth the time at the beginning to lay things out very carefully. The investment we make with extra time spent delving deeply into the fundamentals of our discipline is justified by the rich results shown on conceptual tests [1, 2]. We must find the time to teach well.

How can we help students to focus first on the interactions? Start at the very beginning of the forces unit. My students’ first lesson on forces in grade 11 involves playing with elastic bands. They explore the effect of the elastic on their fingers, with the goal of noticing that two similar forces are involved in the single elastic interaction.



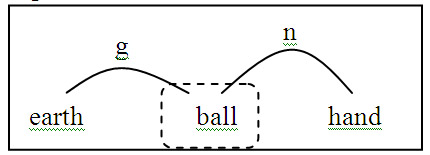
Shortly after, we develop a new tool, the interaction diagram (sometimes called a system diagram or system schema [3, 4]), which visually represents the interactions between each object. Students begin by listing all the objects involved in the situation. Next they draw lines between the objects which represent each interaction. These lines are given single-letter labels indicating the type of interaction, the same labels that will eventually be used on their force diagrams (g = gravity, n = normal, and so on). An ID (interaction diagram) is a very schematic and abstract representation of a situation, but it proves very valuable when it comes time to construct the force diagram. (Incidentally, I never refer to force diagrams as free-body diagrams anymore. Does the term “free-body” mean anything to our students? Don’t teach them meaningless things!)



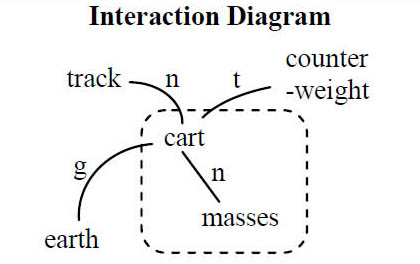
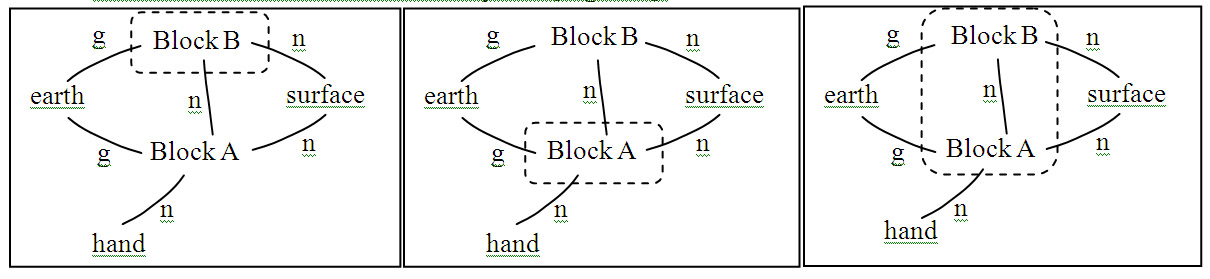
Consider the example of a dynamics cart, with masses on top of it, rolling on a track. The cart is being pulled by a string attached to a counterweight hanging over a pulley. The objects involved are the cart, masses, counterweight, track and earth. We don’t consider the string to be an object since the string is “massless”. Moreover, the strength of the frictional interaction is small compared with the other interactions, so we ignore it.

Before a force diagram (FD) can be drawn, we need to focus our physics lens by choosing a system to study. Introduce students to the idea of a system: a collection of objects whose properties we will track. Other objects in our situation that are not included in the system are part of the environment. We can choose the cart and masses as a system of objects and draw a dashed line around them in the ID. With the help of this system boundary, we can classify the different interactions as either internal (between system objects) or external (between a system object and the environment) to the system.

Explicitly introducing systems early in the force unit is crucial to the development of deep understanding. Choosing a system is a good example of the “hidden curriculum” — a key element in expert thinking that is often never explicitly taught. Instead, we expect students to acquire it through their own diligent practice. They seldom do. Choosing the correct set of objects to group as the system and understanding the consequences of that choice is both subtle and powerful. I used to routinely see my students flounder with this in multi-object problems like the classic “find the force in hitch between the 10th and 11th train car” problem. Students often first encounter the idea of a system when they meet the topics of energy or momentum. I used to jump right in, talking about closed or open systems while my students were simply wondering what a system is — yikes! Using the system concept throughout the topics of force, energy and momentum helps to cement a deep connection between these seemingly distinct and unrelated concepts.

Now we can finally construct a FD! Drawing the ID will quickly become second nature for students if you make them practice it. Only then will the ID serve as a useful primer for thinking about the forces. Begin a FD by representing the system as a point particle — not a box. This helps to make clear a fundamental assumption that we routinely choose in introductory physics: our mental model of most objects or systems is that of a point particle possessing the mass of the system but no noticeable physical dimensions. (The point particle is similar to an object’s centre of mass, but I do not mention this. The concept of centre of mass should be explored carefully as a bridge between the point particle model and the analysis of extended bodies, but we do not cover extended bodies. Note that the point-particle model is not capable of experiencing torques and rotation. All models have limitations, but this one can easily be extended to a point particle and lever arm when necessary.) Once the system is represented by a point, draw vector arrows that represent any forces acting on a system object from external interactions. Scale is not important for the force vectors, but our diagrams should make it visually clear which forces are equal in size or which might be greater. Draw multiple forces vectors acting in one direction tip-to-tail. This helps connect what students learned about vector addition when studying two-dimensional motion and makes visually clear, for example, how all the upwards forces compare in size with the downwards forces.

Consider the problem below (one that I like to use with the OISE pre-service teachers) and ask yourself which answer your students are most likely to choose]:



Most students are convinced that there are three forces in this situation: a gravitational force, a hand force and an “up” force. The ID for this situation is shown below].


Training students to start with IDs is a good way to get them thinking that there is only one interaction between the hand and the ball, which must be the normal force. (Part of the problem here is that students often don’t understand that the “applied” force is just a normal force.)

The real power of interaction diagrams is illustrated in the next two examples from grade 12. Consider the classic two-block question pictured below. A hand pushes horizontally on the first of two blocks, causing them to accelerate along a frictionless surface. (This type of situation should be treated only in grade 12. While you can have grade 11s mimic demonstrated solutions to this problem, they won’t understand it.)


If we were to ask your students what forces act on block B, what would they say? Many would say the push of the hand, of course! Time for an ID with block B as the system].


Taking time to carefully think through the ID prompts students to recognize that the hand only interacts with block A. From the ID the student can see that there are three external interactions with block B and none of them involve the hand. Now they have the correct starting point for a FD. The dividends from the ID investment continue to accumulate if we ask the student about the forces on block A. Since the third law is built into the ID, the student is naturally led to consider that block B also pushes on block A. A quick change of system highlights the four external interactions with block A and a careful FD can be produced. But wait — there’s more! Chances are we are interested in the acceleration of the collection of boxes. Here the system idea shows its greatest power. Choose the system to include both blocks. Since the system (a point particle) has the combined mass of the two blocks, we can draw one gravitational force, one normal force due to the surface and one normal force due to the hand. The interaction between block A and B is now internal and does not appear in our FD. Students learn that choosing a different system has a dramatic effect on the FD.

Switching between different systems for the same situation is a powerful problem solving tool, especially if all the system objects are constrained to move together with the same acceleration. Such a system is a composite object — a useful label. Now you can refer to an Atwood machine as a composite object and this label has important meaning for the students. Now (and only now!) can a student learn how to skillfully choose a system for one purpose (to find the acceleration) and then switch to another (using the acceleration to find a particular force). Does all of this seem a bit complicated? Yes? That’s because it is! And we have been asking our students to basically figure it out without any of this support. Before I used IDs I told myself that my students just need to practice FDs enough and they would understand. This never happened. The better students simply memorized the solution process. That was poor teaching.

Push yourself out of your comfort zone and try out interaction diagrams. It did take me a while to get used to them and to figure out how to teach them, but they now find a place at the core of my teaching praxis. You, however, can take a peek at how I implemented them in my grade 11 and 12 courses and save yourself much of that trouble! All my electronic course materials are available online at www.meyercreations.com/physics. If you would like to see IDs in action, just drop me a line and we can arrange a visit to my class. The door is always open.

Chris teaches physics at York Mills C.I. in Toronto. He runs a reformed physics program that applies physics education research to the classroom.

1. “Using the System Schema Representational Tool to Promote Student Understanding of Newton’s Third Law”. AIP Conf. Proc. 790, pp. 117-120 (2004). http://proceedings.aip.org/resource/2/apcpcs/790/1/117_1?bypassSSO=1
   
2. “Does using a visual-representation tool foster students’ ability to identify forces and construct free-body diagrams?” Phys. Rev. ST Physics Ed. Research 9, 010104 (2013). http://prst-per.aps.org/abstract/PRSTPER/v9/i1/e010104
   
3. “Do students use and understand free-body diagrams?” Phys. Rev. ST Physics Ed. Research 5, 010108 (2009) http://prst-per.aps.org/abstract/PRSTPER/v5/i1/e010108
   
4. “System Schemas”. The Physics Teacher -- October 2003 -- Volume 41, Issue 7, pp. 404 http://tpt.aapt.org/resource/1/phteah/v41/i7/p404_s1?isAuthorized=no