Don’t be so dense!

There is not much that is intuitive about Newton’s laws. Don’t be seduced by the elegance and power of these three laws according to your experienced and expert perspective. Their framework is logical once you buy into it, but looking at force and motion without Newton’s insight is very challenging. Just ask Aristotle (or his mom, who kept his report cards).

Newton’s laws are conceptually very dense. Each law is rich with concepts and cannot be mastered, or even vaguely understood, until each concept is carefully met and dealt with. As physics coaches, we can’t properly train our students until we give them the chance to unpack the laws and explore them in detail. This requires a considerable investment of time compared to my old three day whirlwind tour. Thinking back to those tie-wearing teaching days, at the time I did remark that my grade 12 students had difficulty with physics problems not because of the challenges of pulleys or frames of reference, but because they didn’t understand the “easy” stuff, the first law. I now understand that this wasn’t due to lack of effort on their part. (No one would accuse Aristotle of lack of effort). I simply had not provided them with the right opportunities in which to learn. Now I spend about four days helping the grade 11s build the first law alone.

Blowing law chunks

Let’s borrow a handy idea from psychologists called “chunking”: taking a complex data set or idea and breaking it down into smaller, more manageable parts that help you to better understand or work with the whole. Mathematicians do this all the time, creating systems of lemmas and corollaries that orbit a central theorem. As physics teachers we need to unpack each of Newton’s laws and break down its ideas or implications into meaningful, digestible parts.

I find the first law to be the most conceptually dense of the three. A thorough high-school level understanding of it depends on a slew of wide ranging ideas. I call one chunk of the first law the catalogue of force-motion relationships.

The First Law Catalogue of Force-Motion Relationships

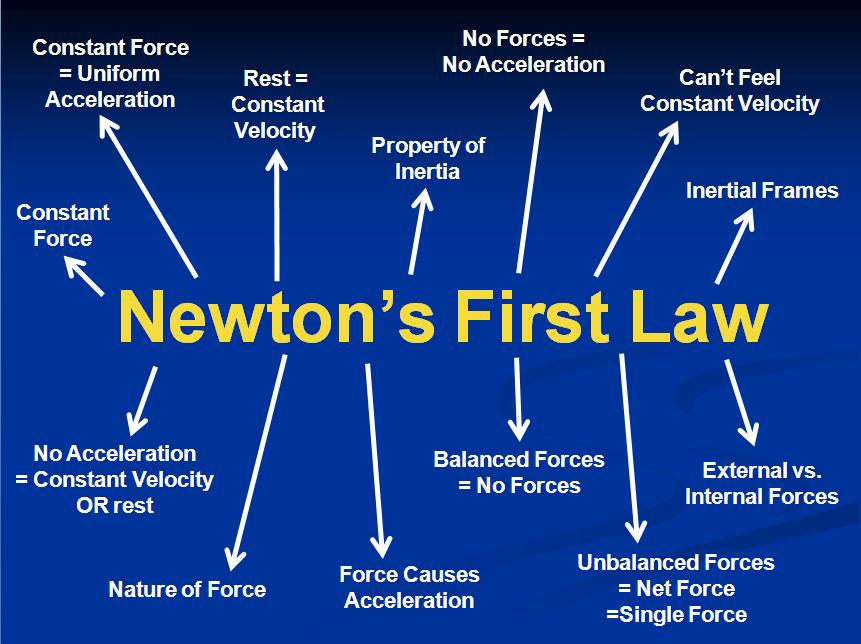
Forces	Motion
No forces	rest or constant velocity
Balanced forces	rest or constant velocity
Single force	acceleration
Unbalanced forces	acceleration

None of the items in this catalogue are obvious or intuitive. It took many people many centuries to find these relationships. A student’s intuitive catalog of force-motion relationships would look more like this:

The Intuitive Catalogue of Force-Motion Relationships

Forces	Motion
No forces	comes to rest or at rest
Balanced forces	certainly at rest
Single force	steady motion
Unbalanced forces	maybe acceleration, maybe steady motion

Students need to deliberately analyze each of these force-motion relationships and draw these connections. This takes two classes for my students. I call another handy chunk the net force principle. When we study the combined effect of many forces acting on a system we routinely think of the system behaving as if it were subject to one single force, the net force. This is an idea so obvious to us experts that we seldom bother to articulate it. Features like this are often called the hidden curriculum. Teachers typically expect students to pick up on the hidden curriculum through practice and familiarity. This seldom happens, leaving students conceptually handicapped.

One final chunk connected to the force-motion catalogue is an idea describing the change between the force states. I call this the force-change principle. When the forces change (for example, from balanced forces to unbalanced forces) the motion changes simultaneously. There is no lag or delay. When we push a box with a constant velocity and then remove the pushing force, the box doesn’t continue on for a while (Aristotle’s impetus theory) before friction kicks in and the slowing begins. (Homework: ask your students to describe in detail what happens in this situation. Their answers are often interesting!)

There is a chunk of the first law that perplexes me: inertia. First of all, I’m not sure why the first law is a law of inertia (reader feedback, please!). The catalogue of force-motion relationships seems pretty complete to me without a mysterious “inertia” thrown in; these ideas don’t depend on the amount of stuff or matter involved. As long as we are not talking about “light” (massless) objects the full catalogue is valid. Secondly, the typical definition of inertia is not helpful: the “resistance of an object to a change in velocity”. What exactly does this mean? Does “resistance” mean that inertia prevents a change in velocity? Does it mean that inertia has to be overcome, like a force of static friction, and then velocity begins to change? How would an intelligent non-physicist interpret that definition? There is nothing that guides one in the use of the inertia concept; this is not an operational definition. Students routinely abuse the concept of inertia, treating it as if it were a force or using it as a blanket “explanation” for all manner of mysterious phenomena. “It happens because of inertia”. No doubt you’ve heard that. (Homework: think of all the events you have heard students “explain” using that phrase.)

The term “inertia” should be retired from introductory physics. Let’s give it a nice party, talk about old times and then walk it to the door. Its close cousin, mass, is a fine concept with a respectable pedigree from Newton’s second law. There is, however, an idea that we need to capture, a new chunk to identify. This chunk points to the real meaning for our retired concept of inertia. Given a non-zero net force, it takes time for the velocity of an object to change. The interval of time can sometimes be very small, but it can never be zero. The amount of time is related to the system’s mass (hinting at the second law). I call this the inertia principle out of nostalgia; it could also be called the velocity-change principle. This targets the idea inertia was traditionally meant to explain. It also helps remind students what is actually happening when a collision occurs or an object “suddenly” stops. These processes don’t happen instantly; they require an interval of time. This also helps to remove the apparent differences between continuously acting forces (the constant forces we like to study) and short, impulsive forces which can seem very different or go unnoticed entirely. For the record, my students don’t really remember the phrase “the inertia principle”. But they do say things like, “No, it doesn’t happen instantly. It takes time for the velocity to change.” Compare that with “it happens because of inertia”. Which demonstrates a better understanding? (Homework: try out this principle when you perform the table cloth and dishes trick.)

After the careful preparation of several days spent on the first law students are primed for the second law. They have a clear idea of the net force and its special connection with acceleration. They also know that mass is the special mediator between force and acceleration, naturally leading to the question of how mass affects the resulting acceleration. I give the second law the nickname of the law of cause and effect. This nickname helps prevent students from making errors of reasoning that are mathematically logical but physically bizarre. Consider an equation from math class like z = xy. What happens if you double x? Clearly, z doubles as well. Give a student the equation F_net = ma and ask what happens if we double the mass in a given situation, they may actually say that the net force will double! Emphasizing the idea of cause and effect helps guide students in the use of these symbols, cuing them to reflect on the physical constraints of the situation rather than the mathematical structure of the law alone. (Homework: think of other equations where students commonly forget the physical constraints and interpret them in a naïve, mathematical way.)

The real excitement of the second law comes from its vector nature. It may be easy to understand that the direction of the acceleration is the direction of the net force (which I drill during the first law). But what if the net force is not parallel to the velocity? Panic! When students meet projectile motion in grade 12 (don’t even consider it for grade 11) we need to extract a new chunk from the second law. Students need to explore in a concrete way how the velocity vector changes when the net force is no longer parallel to it. (We use hoverpucks on a wide incline). Nothing about this is obvious or intuitive. (Homework: ask your students unbiased questions about what they think will happen and you will learn interesting things.) This leads us to our next chunk, the orthogonality principle: a force in one direction has no effect on the velocity in a perpendicular direction. Another way of saying this is that Newton’s first law applies separately to each perpendicular direction.

Soon we reach the very thorny topic of circular motion, which I have treated in the June 2012 OAPT Newsletter. The conceptual foundation for circular motion and all curvilinear motion can be summed up through another chunk, the speed and direction principle: a force parallel to the velocity changes only the speed; a force perpendicular to the velocity changes only the direction. Once students are confident that a component of a force still counts as “a force” this principle becomes very powerful.

Consider this typical definition of the third law, courtesy of a ministry approved textbook. (Spoiler alert: I don't like this definition.)

"For every action force there is a simultaneous reaction force that is equal in magnitude and opposite in direction,"
from Physics 11, Nelson (2011).

If you ask a typical physics student, "What do you think action and reaction mean?" what would he likely say? How would he interpret these terms? Not the way we do, guaranteed! He might come up with ideas like "cause and effect", "first this, then that", or "something moving or impulsive". The choice of language in this definition is very problematic. Including the word “simultaneous” to appease the physics lawyers helps about as much as holding the brakes while hitting the gas.

How about this definition from the other approved physics textbook:

"If object A exerts a force on object B, then B exerts a force on A that is equal in magnitude and opposite in direction,"
from Physics Source 11, Pearson (2011).

This seems to be an improvement, except that in the following paragraph they go on and on about action and reaction forces! Zounds! In this definition there still is a problem with causality implied by the "if - then" construction. We are still left with the impression that one force happens first and the other happens as a response.

We need some serious redaction on the words “action” and “reaction”. They should be banned from discussions of the third law! Outlawed! To better describe the third law we need the concept of interactions, which I described in detail in the last OAPT newsletter (inverse-spoiler). This forms the core of my definition of the third law. So long as we are not considering fields, the third law can be reformulated as:

Newton's Third Law for the 21st Century Whenever two objects interact they exert forces on one another. The two forces from a single interaction form a 3^rd law force pair and have the following properties:

• they have the same magnitude;
• they point in opposite directions;
• they are the same type (gravitational, normal, etc.);
• they arise and act simultaneously;
• they involve the same pair of objects;

This understanding of interactions is known as Newton's 3rd Law.

Another feature of my previous article is a tool that helps students think about these interactions and "see" the third law. Imagine a doll resting on a table. The interaction diagram shows the four important interactions that are present in this situation. Each interaction line represents a pair of forces, a third law pair. For example, the line between the doll and table represents the normal force interaction between these two objects and implies a mutual influence of each object on the other.

So you think everything is fine and your students are happy with a new definition of the third law. Then you give them this question as a check:

Guess what they answer? By the end of grade 12 after much careful intervention, only 74% of my students choose the correct answer to this question. (Which is?) Students have a very deeply held belief that the third law doesn’t apply to situations like this. In grade 11, before we develop the third law, I give my students four situations (illustrated using the Smart car and the tow truck, below) and naively ask them which forces exist (force of car on truck, truck on car) and how their sizes compare. Then they pool their results on the chalkboard. The pooled results from my class of 30 and two individual student results are shown below.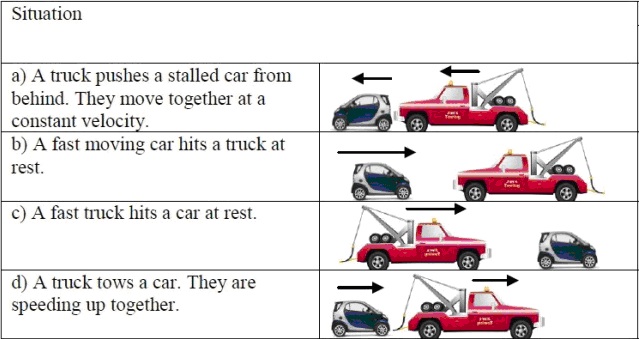







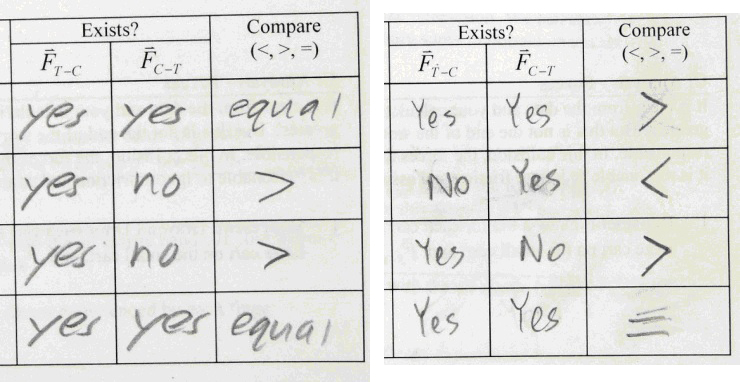
Notice how for situation C they very strongly favour the truck exerting the larger force. When applying Newton’s third law to situations, students are often led astray in the following ways. They think that:

• the “stronger” object exerts a greater force
  

• the moving object or a faster-moving object exerts a greater force
  

• the more active or energetic object exerts more force
  

• the bigger or heavier object exerts more force
  

This brings us to what I call the third law conundrum: if the forces in a third law pair are always same size, why are there such different results for the two objects involved? Three common reasons are the differences in mass of the objects, differences in velocities, or one object experiences other forces. We need to lead students through an examination of these situations to try to help them reinterpret their common sense and personal experiences. When they notice that the Smart Car gets clobbered by the truck, we need to help them understand that they are not observing forces; they are observing the results of forces, meaning the accelerations. Their intuition is not wrong – the smart car does get clobbered. Instead they need to develop new physics ideas and re-examine familiar situations in the new light of their growing understanding.

Create a special forces unit for your grade 11 and 12 courses using our reformulated laws. Start your beginning physics students off right. We use the Force Concept Inventory at our school to help track student understanding of acceleration and forces. Our historical average (five semesters) for students beginning grade 12 has been 53.0%. Having made these changes to the grade 11 course, our new grade 12 students this fall have scored 59.8%, making for a statistically significant improvement (two-tailed student t-test = 0.026, n=53, Cohen’s d = 0.34). Try this out for yourself and see the difference. Or drop by my class to observe the PERsuasive teaching of forces in action.

We teachers forget what it’s like to tackle Newton’s laws for the first time. It is challenging and exciting for students when done well. Listen to your students talk about forces and you will hear many of the points I have mentioned in this article. Check out my online resources (www.meyercreations.com/physics) to find my complete lessons. Challenge yourself to use these new ideas to help your students improve.