Adam Mills, Teacher Assumption College Catholic High School
adam_mills@wecdsb.on.ca

I am going to write a two part series of articles in which I discuss the ideas of Cooperative Group Problem Solving (CGPS) and how I use these in my classroom. In part one of the series the foundation for what CGPS encompasses will be discussed and in part two, I will go into more detail as to how I use it in my classes. These topics were discussed in my presentation at the OAPT conference this year. You can find the slideshow as well as extra resources at http://bit.ly/OAPT2017.

After teaching for a few years I started to ask myself what is the purpose of Physics Education? That is, what do I want my students to take away from their Physics classes? Why is it that every single Bachelor of Science Degree or Engineering Degree requires their first year students to take Physics? After speaking to many colleagues I began to realize that Physics provides us with a framework through which we can solve problems. Now when I refer to problem solving I am not referring to simple questions that involve substituting numbers into an equation and applying some mathematical manipulation. I am referring to the situation where, after reading the question you do not immediately have a way to begin your solution. I am referring to questions that require the students to stop and think about what they are being presented with, what is the question asking them to find and what is the important information they are being given?

After some research into problem solving in Physics it became evident that the type of problems that lead to these sorts of challenges for the students are referred to as context-rich problems. I also realized that such complex problems cannot be given to my students without providing them with a framework for approaching these challenging questions. Much of the legwork for providing this framework was completed by Pat and Ken Heller from the University of Minnesota³.

Two of the essential points made by Heller and Heller to assist in aiding our students’ problem solving abilities were to:

• Have the students work in groups.
• Provide the students with a problem-solving framework and then insist that they follow this framework at all times, including during a test.
  

The remainder of this article will focus on how I complete the first two parts in my classroom.

Task #1: Creating Cooperative Groups:
A lot of upfront effort is spent on assisting my students to be able to successfully work in groups. During my first few years of teaching I had always assumed that by grade 11 my students would inherently know how to work in groups… I was very, very wrong. Once I started observing their behaviour when placed in groups I quickly realized that they thought group work meant divide and conquer. They would assign each other a task that they would work independently on; they were looking for efficiency. In the rare event that they would try to work with each other, I found that the students were not capable of resolving conflicts on their own. They would often confuse ‘not agreeing’ with ‘not liking’ an individual. Finally, they would seldom listen to the other group members’ opinions, but instead they would be thinking about what they were going to say next. In order to combat these behaviours I spend my first two classes of each semester leading the students through a process of how to work appropriately in groups.

During these first two classes I repeatedly stress the following points;

• They were not put into groups in order to divide and conquer, but rather to provide them with the opportunity to discuss their ideas with their peers. This allows every student to be more actively involved in their own learning process. Furthermore, real world problems are usually too hard for any single person to solve, thus being able to share and listen to ideas is vital for their success after high school.
• Their peers are their primary source for ideas and answers. They should only ask the teacher for assistance if the group cannot obtain an answer after they have put forth a reasonable amount of effort.
• Every group member has a specific role to play. These roles — based on the work by Heller and Heller — include Manager, Recorder and Skeptic. The details of each role can be found in the table below. If there are four members in the group, there are two Skeptics. These roles alternate on a daily basis and the teachers needs to put in a lot of effort at the start to ensure that every student stays within their role. This helps to ensure that a dominate student does not constantly take over a group.
  


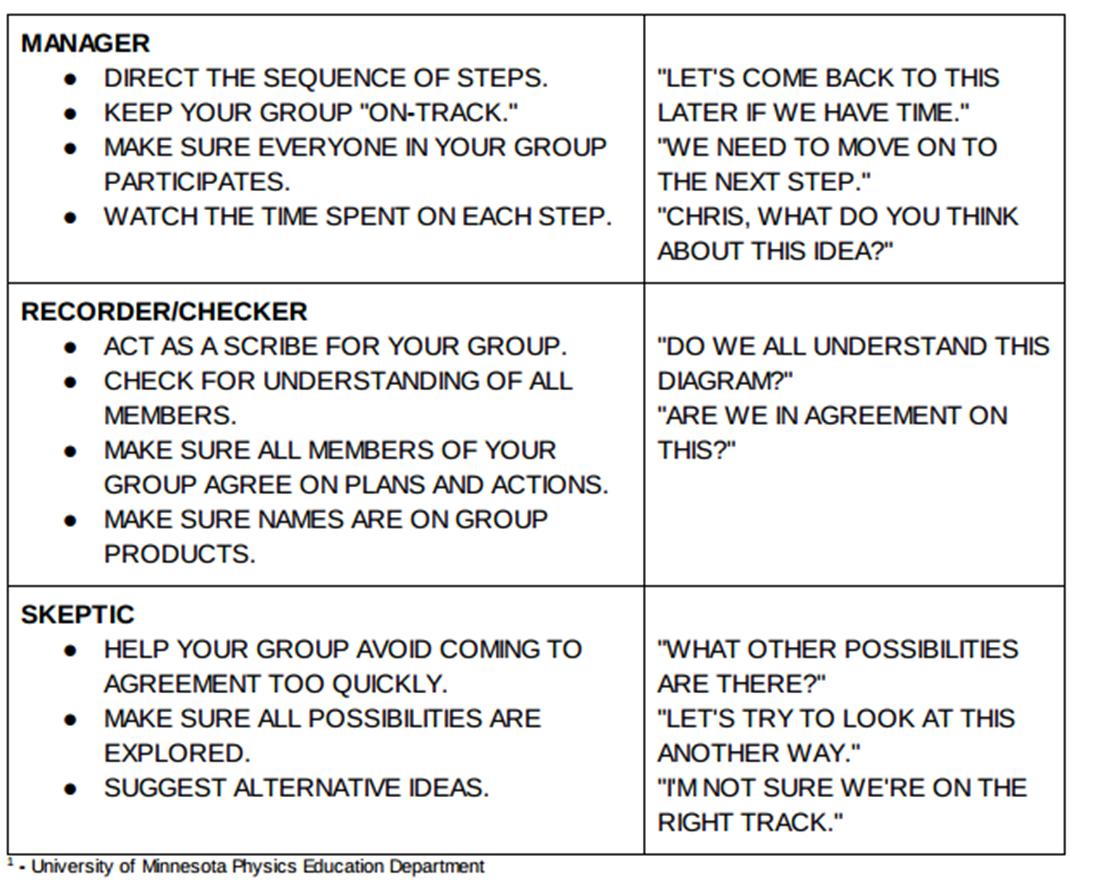
The above table is posted around the room and many of the phrases are posted at each table to provide scaffolding for the students and constantly remind them of how to successfully complete their role.

• I encourage the use of specific phrases to show that the group members are engaged and actively listening, such as “What I heard you say was…”.
• I emphasize the importance of being aware of their body language. For example making use of appropriate eye contact when someone is speaking rather than looking at the problem or the whiteboard. Leaning in towards your group mates instead of sitting back in a chair or slouching, demonstrates that you are engaged in what the other person is saying.
• They are required to make use of their whiteboard as a common space for working through ideas.
  

When creating groups, I make use of the research of Peter Liljedahl² from Simon Fraser University. His work demonstrates that randomly assigned groups provide the greatest advantage to the students. So in my class I have a random selector (which is small box filled with the numbers 1 – 8) and the students will select their group number as they enter the class on the first day. The groups are then changed every three weeks or more frequently if I feel it is necessary.

Task #2 - Providing a Problem Solving Framework.
When students are asked to solve problems they often use novice problem solving strategies. As Heller and Heller3 discuss, these strategies frequently fall into one of two categories which they call Plug and Chug and Pattern Matching.

The typical Plug and Chug approach might follow a sequence as shown below.



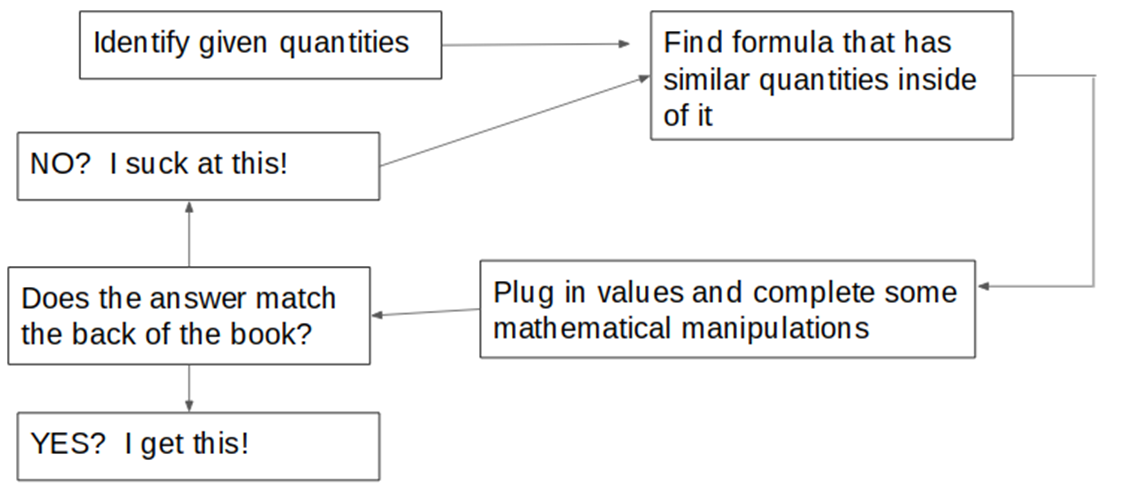
Students using this approach are frustrated with the number of formulas that they need to memorize or the amount of material presented. This is because they are focusing on all the different types of problems that they are exposed to rather than the overarching physical concepts that connect many of these problems. To an expert an inclined plane problem is similar to a pulley problem because both require Force Diagrams and the application of Newton’s Second Law. However, to many of our students these are two completely different problems.

Students who apply the pattern matching approach — which are sometimes my stronger students — will attempt to solve a problem using an approach that worked in another situation that they deem similar. When presented with a context-rich problem, these students will often state that they do not know how to start.

In order to move our students away from these novice strategies and towards expert strategies we need to provide them with a framework that they can use when presented with a new problem. The framework that I use is based on the work by Randall Knight1 in his fantastic book Five Easy Lessons: Strategies for Successful Physics Teaching. The essential idea of this framework is based on the idea of Multiple Representations. Like Chris Meyers⁴ I provide my students with a solution template in order to scaffold this approach.  

The basic idea behind Multiple Representations is to require students to actively think about the problem from as many perspectives as possible. Like Randall Knight and Chris Meyer, I have my students complete three major representations.

1. Pictorial Representation: definition of events/system, sketch of problem with events labeled on diagram, label knowns and unknowns using appropriate variables, coordinate system, conversions.
2. Physics Representation: x - t graphs, v - t graphs, motion diagrams, Force Diagrams, Interaction diagrams, energy flow diagrams, energy bar charts, velocity vectors etc., what are the important physics concepts?  What assumptions did you make if any?
3. Mathematical Representation - Explain what you are doing and include Equations, algebraically isolate for unknown, numbers substituted in with units, consideration of size of answer.
   

They do not need to memorize what is included in any of the representations, they are constantly provided with these reminders on every solution template and they are posted around the classroom. From unit to unit, the only representation that changes in content is the Physics Representation. For example, the Dynamics Unit would include velocity-time graphs, Interaction diagrams and force diagrams, whereas the Energy Unit would use energy bar charts and energy flow diagrams.

Looking at the requirements for each representation you can clearly see that a lot is required from the students for each problem that they solve. Therefore, I do not assign very many problems for homework. Instead, they must do a few problems really, really well. As Vince Lombardi once said, “Practice does not make perfect, perfect practice makes perfect.” Any time the students are required to solve a problem, it must be done using this method or it will not be accepted. It is very important to be consistent with this requirement, including test situations! You can view an example of my Energy Solution Template by following the link provided at the beginning of the article and clicking on the shared Google Drive.

By having the students consistently apply this problem-solving approach we are creating a method by which they can begin to solve any type of problem. We are scaffolding the problem-solving approach and helping to move them away from their novice strategies. Notice how the mathematical representation does not occur until the end. So many of our students want to rush the math first without thinking about the physics and this approach can be successful with many standard textbook problems. Therefore, if we want our students to buy into the above problem-solving strategy we must provide them with problems that prevent the standard plug and chug or pattern matching approach. As mentioned these types of problems are referred to as context-rich questions. How I use these types of questions in conjunction with groups and multiple representations will be discussed in the next article.

References:

1. Knight, Randall D. Five Easy Lessons: Strategies for Successful Physics Teaching.  Addison-Wesley, 2004
2. Liljedahl, Peter, ‘The Affordances of Using Visibly Random Groups in a Mathematics Classroom’.  Research Gate, https://www.researchgate.net/publication/275953522_The_Affordances_of_Using_Visibly_Random_Groups_in_a_Mathematics_Classroom.
3. Heller, Pat and Heller Ken, ‘Cooperative Group Problem Solving’, University of Minnesota, http://groups.physics.umn.edu/physed/Research/CGPS/CGPSintro.htm.
4. Meyers, Chris, ‘Solution to the Problem solving Problem’.  http://www.meyercreations.com

Tags: Pedagogy