Al Bartlett, University of Colorado

Fill a one-litre graduated cylinder with water; the cylinder should be about 5 to 8 cm in diameter and 30 to 40 cm tall. Take an ordinary glass marble and try to drop the marble into the water in such a way that the marble will fall all the way to the bottom without first hitting the side of the cylinder. The marble makes an audible click every time it hits the glass wall.

The marble is always drawn to the wall — it bounces off and then hits the opposite wall. I have never seen one go down without first hitting the wall.



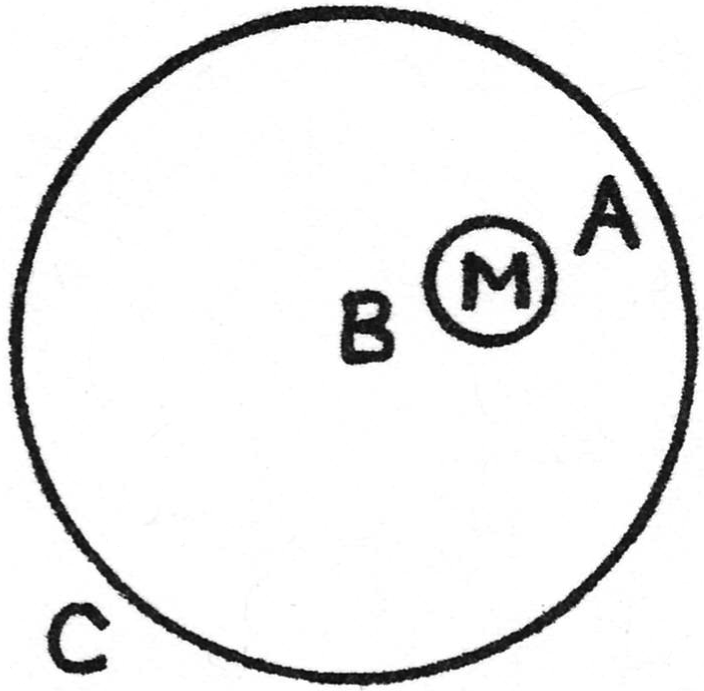
I believe the explanation is this. If C is a horizontal cross-section of the cylinder and M is the marble, then an observer on the marble will see water flowing upward all around the horizontal equator of the marble. But, because of the proximity of the wall, the upward flow velocity at A will be greater than at B. By the Bernoulli principle, the pressure at A is less than at B, and the ball is moved to the nearest wall. As the gap narrows, the force increases — and the marble strikes in an approximately elastic collision, and bounces away from the wall with sufficient velocity to cause it to move out.

In principle, one should be able to drop the marble exactly on centre — just as you should be able to make a sharpened pencil stand on its point. In practice, of course, this is impossible.

I first saw this demonstration performed by William B. Pietenpol of the University of Colorado (Boulder).

Column Ed. Note: Al Bartlett sends his best wishes to all his friends in the OAPT. He still goes out on the road giving his exponential-growth talk, which he presented 62 times last year.

---

Column Editor: Ernie McFarland, Physics Department, University of Guelph, Guelph, Ontario, N1G 2W1

Tags: Fluids, Pressure