George Vanderkuur, WICED Centre, TDSB
georvand@enoreo.on.ca

Bricks, books, or metre sticks are all you need for this neat demonstration. As illustrated, the top brick projects by half its length and subsequent bricks project 1/4, 1/6, 1/8, et. Brick lengths. After n bricks, the cantilever will project a distance of d = 1/2 + 1/4 + 1/6 + … + 1/(2n). This may be simplified to d = 1/2 (1 + 1/2 + 1/3 + … + 1/n). For four bricks, the projected distance is 1.04 brick lengths, and for n = 5, the distance is 1.14 brick lengths (so that the top brick is clearly out beyond the edge of the table).



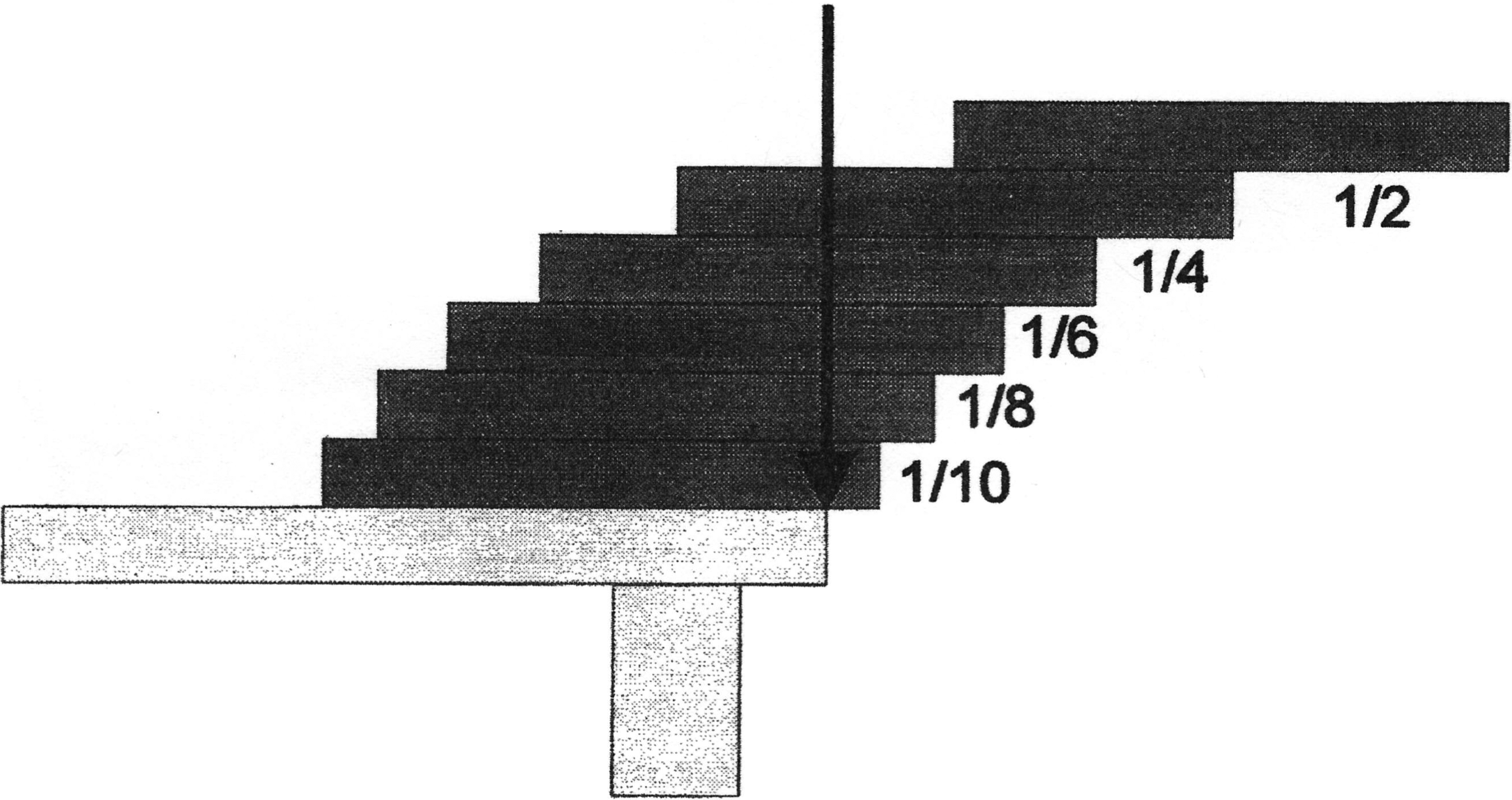
There are numerous complicated ways of determining the maximum projection for each brick. Even though the physics is simple, the equations soon become unwieldy, requiring clever techniques that I have forgotten. There is, however, an easy way to look at the problem. Just consider the total projected mass at various levels in the stack. Above the second brick from the top, there is one-half brick mass projected. Above the third brick from the top, there is the half brick mass just mentioned, plus two quarters (one quarter from the second brick and another quarter from the top brick). Above the fourth brick from the top, the total projected mass is one half plus two quarters plus two sixths. This arrangement ensures that the cantilever exactly balances on the front edge of each brick because at each stage an additional half brick mass is added to the total overhang. The centre of mass of the projected portion is balanced by the centre of mass of the rest of the stack. (You might want to think in detail about how this scheme works once two or more bricks are completely projected beyond the table edge, so that they can’t contribute any more projected mass.)

Is this device practical?
Not really — the structure soon fails because the load is carried entirely at the front edge. The compression forces are greater than what normal materials are able to withstand. Disregarding this, the cantilever could ectend to infinity because the sum 1/2 (1 + 1/2 + 1/3 + … + 1/n) has no limit. It would take 100 bricks to extend 3 brick lengths, and to extend 10 brick lengths would take over 1,000,000 bricks.

It is hard to imagine how a loose stack of bricks could extend out infinitely far. It should make for a lively discussion.

---

Column Editor: Ernie McFarland, Physics Department, University of Guelph, Guelph, Ontario, N1G 2W1

Tags: STEM