John Wylie, The Toronto French School

Here is a good demonstration that can be used in its simplest form to show stable and unstable equilibria or, in a more advanced version, to illustrate some finer points about moments of inertia and angular motion. The material needed could not be simpler. You need a board. There are no special requirements here except that the board be rectangular and have three distinctly different dimensions. In a pinch, I have used a good-sized physics text book held closed by a strong elastic. Most brief cases work and if students feel lucky, they can try out their calculators.

The demonstration starts out by showing that a rectangular object has three principal axes (label them x, y, and z) about which it can rotate.



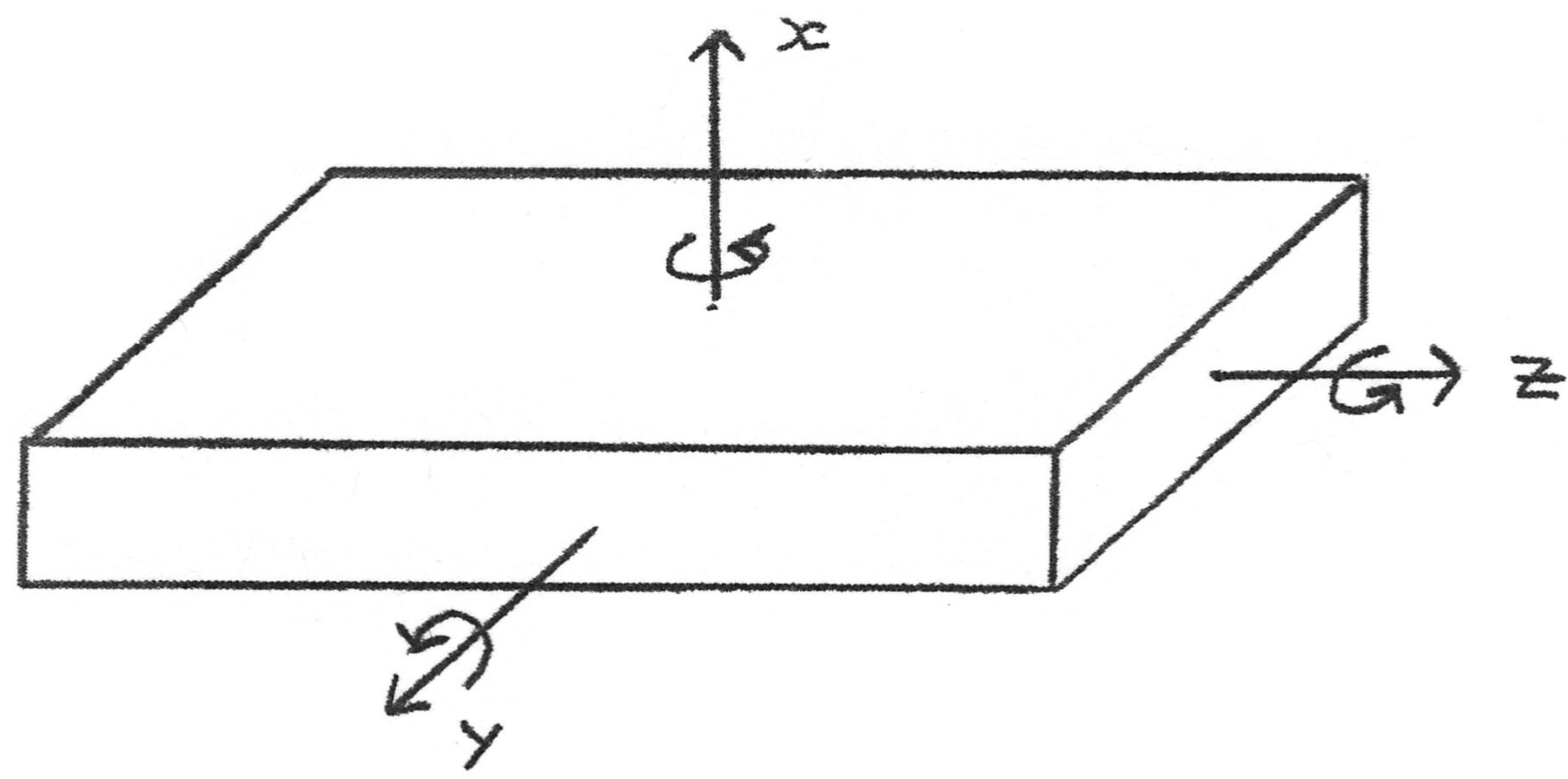
If you are teaching moments of inertia, you might have the students classify these axes by increasing moments. For our purposes, we note that I_X > I_y > I_z. Now toss the board up into the air giving it a good spin about the x-axis and have the students note its nice stable rotation. You will have to practice this a bit to give the board enough spin and hang-time for the stability to be evident to the whole class. Do the same for the z-axis and then pick a volunteer from the class and challenge him or her to repeat the trick for the y-axis. A rotation about this axis is unstable and will quickly decompose into a combination of rotations about the other two.

Students are always curious about unstable systems. At the very least, it is worth getting across the concept that an unstable equilibrium will (due to the slightest perturbation from anywhere in the universe) degenerate. Let them try the y-axis spin until they have satisfied themselves of this. The explanation of the effect follows and uses concepts from angular momentum and energy, both of which must be conserved while the object is spinning freely in the air. Conserving energy is the easiest and gives us



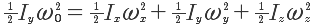
We assume here that the board was given an initial spin about the y-axis with initial angular speed wo. We look for a final situation in which the board may be simultaneously spinning about any and all of its principal axes. Since angular momentum is a vector, it is a bit pesky to write its conservation equation directly. It is much easier to write the equation corresponding to the conservation of the square of the angular momentum. This gives



If we multiply the energy equation on both sides by I_y and combine it with the angular momentum equation to eliminate Iy2ω02, we can arrive at



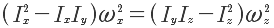
Since I_x > I_y, > I_z, both sides are positive and a solution exists for ω_x and ω_z. If we repeat the above calculation to ask for the case where the initial spin was about, say, the x-axis, we find



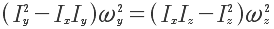
In this case, the left side must be negative but the right side is positive. The only solution is ω_x = ω_z = 0. One would find the same thing for an initial spin about the z-axis.

The above analysis does not require that we be studying a rectangular board. Generally, objects spinning about axes corresponding to their greatest and least moments of inertia will be stable whereas a spin about its third axis will be unstable. Objects with enough symmetry to give identical moments of inertia for one or more of their axes do not have any unstable spins. Cubes, cylinders and spheres fall into this category. Imagine the problems if a high-speed flywheel had an unstable rotation about one axis. Satellites are also manufactured to avoid these problems.

On the other hand, some objects are made specifically so that when spun, a complex tumble will result. I have seen at least one amusement park ride incorporate this concept: the one where a rider straps into a seat mounted within two gyroscope-like gimbals. The operator gives the rider an initial spin and physics takes over (with usually a little biology mixed in for good measure).

---

Column Editor: Ernie McFarland, Physics Department, University of Guelph, Guelph, Ontario, N1G 2W1

Tags: Motion