Diane Nalini de Kerckhove, Department of Physics, University of Guelph

Diane Nalini de Kerckhove is an Assistant Professor in the University of Guelph’s Department of Physics. She is also a singer/songwriter and recently launched her third CD, “Songs of Sweet Fire”, a collection of Shakespeare songs and sonnets set to her original jazz and blues music.

I have never met anyone who doesn’t like music. After teaching the physics of waves at various levels over the years, I’ve come to realize that demos involving music have a wide appeal with students, especially since most of them have studied an instrument at some point or another. Here are two options for exploring harmonics of standing waves.


Figure 1: Demonstrating the second harmonic on a long spring.

When first introducing the idea of a standing wave, I like to dig out a long spring (at least 2 metres long) and ask a student to hold one end steady. By moving the other end in simple harmonic motion, it is a simple matter to set the spring moving in the fundamental mode (and visually, it looks very much like a giant guitar string). Using a stopwatch, students can then find the average frequency. Finding the second harmonic (shown in Figure 1) is easy enough, and it is useful to slowly increase the oscillating frequency. The erratic movement of the spring as you ramp up from f₁ to f₂ = 2f₁ is helpful in demonstrating that a string of a given length will not sustain waves at frequencies other than multiples of the fundamental. The appearance of the first node between two antinodes always elicits an ‘a- ha!’ reaction. And, with a bit of practice, the third and fourth harmonics can be achieved, demonstrating very readily how nodes are evenly spaced, and added one at a time as one moves through the harmonic series.

At this point I like to remind students that real strings on instruments oscillate in all modes simultaneously, with varying amplitudes. As a jazz singer myself, I first noticed this fifteen years ago when a bassist I was working with plucked an open G string and quickly ‘tapped’ the octave above the note as he slid through an intricate solo sequence. Afterwards, I asked him to show me again how he did it: he simply touched the string (which was still sounding low G) at its midpoint. This damped out the fundamental in the exact position of the node for the second harmonic, which continued to sound, thus producing the octave above the low G.

Using a microphone connected to an oscilloscope with a Fast Fourier Transform setting (for example, the Tektronix TDS 1002), one can monitor sound waves in both the time and frequency domains. If you do not have access to such a scope, there is some simple Freeware software (such as “Frequency Analyzer” available for free download at: http://www.relisoft.com/Freeware/freq.html). This will produce a frequency spectrum for either a microphone input to your computer or pre-recorded sounds (they must be .WAV files). Shown in Figure 2 is a spectrum of a soprano sliding up a scale, using one of the files available from the website for the University of New South Wales’s Acoustics Lab. See: http://www.phys.unsw.edu.au/music/ for more details.

Standing waves and Fourier series can be dry and abstract for many students, but applying them to the acoustics of voices and instruments can help make the subject come alive.


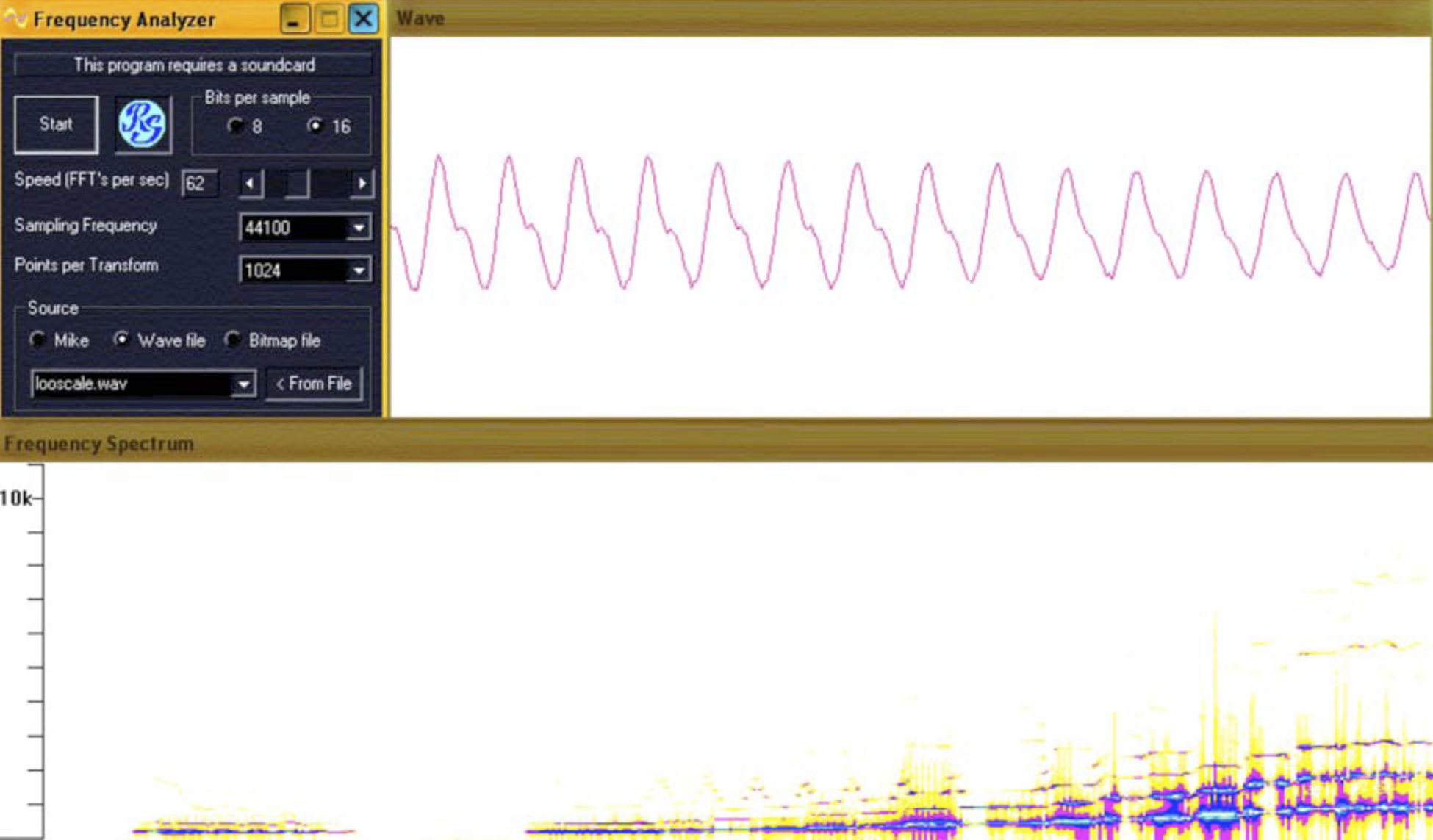Figure 2: A screen capture of the wave form (above) and the frequency spectrum (below) for a soprano sliding up a scale, using the software “Frequency Analyzer.” Time is on the horizontal axis in both displays, and the vertical axis in the lower display is frequency in hertz. Note the significant presence of higher harmonics.

---

Column Editor: Ernie McFarland, Physics Department, University of Guelph, Guelph, Ontario, N1G 2W1

Tags: Waves and Sound