Tetyana Antimirova, Department of Physics, Ryerson University
antimiro@ryerson.ca

One of the ubiquitous simple physics demos that works equally well for all audiences from small children to the students in the introductory mechanics course is a plastic or wooden spool (or yo-yo) with a string wound around it. A virtually no-cost version of the “demo equipment” is a spool of common household sewing thread. Being curious, I did a Google search on yo-yo, and the search produced about 120,000,000 results!



There are many experiments that one can perform with such a spool, but perhaps the simplest one is the most striking. Set the spool on a table to that it is free to roll, with the free end of the string or thread being held at an angle to the horizontal (as shown). Ask your audience to predict in what direction and how the spool will move if you pull the string. If one pulls the string from below, the spool can be made to roll in either direction: forward or backward, depending on the angle of the string with respect to the horizontal surface. The real beauty of this experiment is that regardless of the majority of the audience’s predictions, the spool can be made to roll in the direction that is opposite to the predicted one simply by pulling the string at the appropriate angle! Moreover, while most of the audience usually predicts that the spool will roll, not many see the possibility of it sliding. Yet if you adjust the angle accordingly, the spool may even slide on the surface instead of rolling. If you do this experiment, you will discover that the spool will roll away when you keep the angle between the pulling string and the horizontal surface large enough. The spool will roll toward the string if you decrease the angle beyond some critical value.

If you keep the angle close to the critical value while pulling the string, your audience will not even notice the small change in the angle you make and will be quite puzzled by the fact that the direction of motion of the spool can suddenly change. In order to explore this mysterious behaviour, you can give the spool to small groups of students and ask them to find out on their own how the spool responds to being pulled. Repeating the experiment with a spool of different mass or dragging the spool across a smoother or rougher surface will demonstrate that neither the spool’s mass nor the friction coefficient affects the angle at which the direction of rolling changes. However, the critical angle will be different for the spools with different inner or outer radii.

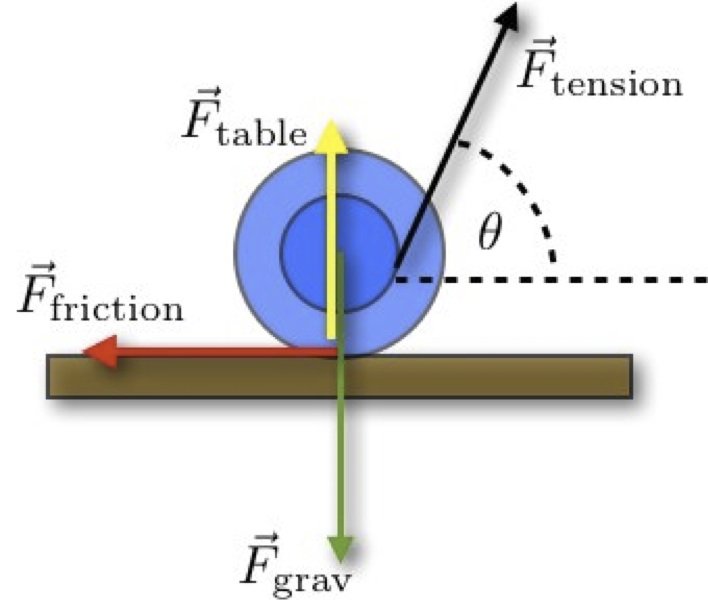
One can just stop here, but depending on the audience’s knowledge background, one can also develop a free-body diagram and proceed with the detailed force and torque analysis to predict the critical angle at which the behavior of the spool changes. The free body diagram shown here is borrowed from the website of Rhett Allain (Southeastern Louisiana University) at http://scienceblogs.com/dotphysics/2010/01/yo-yo_rolling_sliding_pulling.php and corresponds to the scenario where the spool is pulled to the right. Here, r₁ and r₂ are the inner and the outer radii of the spool. Let’s first find out the conditions at which the spool is just on the verge of slipping without rolling. One can identify four forces that act on the spool: weight of magnitude F_grav= mg (down), the tension F_tension in the string due to the pulling, the normal force F_table that is exerted on the spool by the supporting table (directed upward), and, finally, the static friction F_friction force. The tension force makes angle θ with respect to the horizontal direction.



Note that the friction is static (not kinetic), since the spool is not sliding just yet. Close to the threshold of sliding, the magnitude of the static friction force is reaching its maximum value: F_friction = μ F_table where μ is the coefficient of static friction between the spool and table. If the spool is not yet moving, the net force in the horizontal direction must be zero. Therefore, F_tension cosθ = F_friction = μ F_table. In addition to forces, the torques must be considered. Only two of the four forces (tension and friction) produce a torque about the centre of the spool. The spool does not rotate when these torques balance: F_tension r₁ = μ F_table r₂. Dividing the previous equation into the last equation results in the equation that relates the ratio of the inner and outer radii with the critical angle at which the string must be pulled so that it just slides: cosθ = r₁ / r₂. At larger angles the spool rolls away from the direction of pull, while at a smaller angle the spool rolls towards the direction of pull! Note that this equation confirms that the critical angle does not depend indeed on mass or the coefficient of friction.

An alternative qualitative explanation is available if we consider the torques with respect to the point where the spool touches the supporting surface. Only the torque due to the pulling force is non-zero. Even this torque disappears when the string is pulled at such an angle that the line of application of the force goes through the point of contact between the spool and the surface. If one considers the geometry, it happens when cosθ = r1/r2.

This simple inexpensive demo gives the opportunity to discuss several important concepts in mechanics, such as kinetic versus static friction, rolling versus sliding friction, and to analyze how the interplay of various forces and torque lead to different types of motion and more. Enjoy the toy!

---

Column Editor: Ernie McFarland, Physics Department, University of Guelph, Guelph, Ontario, N1G 2W1

Tags: Forces