Alasdair Paterson, Teacher at White Oaks Secondary School
Paterson@hdsb.ca

Last spring, I took my students 2200 years back in time. My grade 8 students measured the size of the Earth using shadows — the technique first described by Eratosthenes.

Historical Background
Eratosthenes of Cyrene (BC 276-195) was a librarian at the library of Alexandria. He knew that the sun was exactly overhead in the town of Syene (now Aswan, Egypt) at noon on the summer solstice (June 21). At this time a vertical stick cast no shadow.


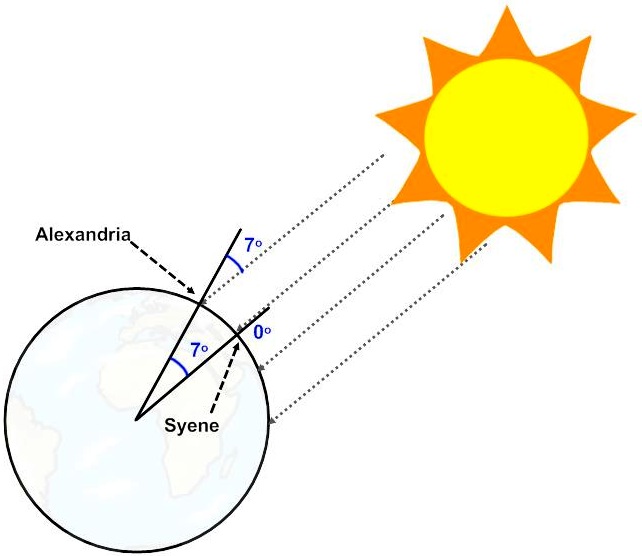Figure 1: The geometry of Eratosthenes' experiment.

At the same time, on the same day, he made a measurement of his own. He found that the shadow of a vertical stick was 7 degrees from the vertical. He used this information and the geometry of triangles and circles to deduce the circumference of Earth (Figure 1). Some say he was within 1% of the actual value, others say he was out by about 15%. Either way, it was a brilliant experiment.

Pedagogical Motivation
I teach a grade eight class in our high school. These students have self-selected for needing aid in the transition from elementary school to grade nine. Most have learning disabilities, some have behavioural disabilities, and all have become disengaged from academics. I have the fortune of teaching these kids both science and math from the perspective of a non-credit bearing course, where the curriculum is determined from a combination of the needs I see in them and the concepts and topics that interest them. The purpose is to engage them and help them transition into grade 9.

I was inspired to try and replicate the experiment after watching Adam Savages TEDEd talk called “How Simple Ideas lead to scientific discoveries”.



I found a willing colleague in Arkansas who agreed to drag his young children out of bed early to do a science experiment.


Figure 2: Adam Hicks and family (of Little Rock, Arkansas) set up their part of the experiment.

At the same time (8:00am Eastern) both parties measured the angular position of the sun in the sky. This involved two measurements: its azimuth and its altitude. Azimuth is the horizontal angle measured between an agreed direction (in this case, compass north) and the celestial object’s position. Altitude is the vertical angle between the horizon and the celestial object.

Experimental Method
Materials used included some tape, scissors, a metre stick, an 8x11 piece of paper, a large wooden protractor, a plumbline (cleverly constructed from about 80 cm of string and six washers), a vertical level, and a compass. The protractor, plumbline, and paper were taped together to form a clinometer.


Figure 3: The clinometer showing a sun angle from vertical of 65°

Angling the clinometer so that the sun was shining directly down the paper tube, we stilled the plumbline then pinned it with a finger to the angle measurement on the clinometer. This was the ‘altitude’ of the sun’s position in the sky. When the clinometer is properly aligned, the shadow of the tube on the top of the protractor is not visible on the ground.


Figure 4: Correct orientation of the clinometer makes the protractor thin and the sighting tube invisible.

Using the vertical level, we set the metre stick up so that it was vertical (measured using the level in both horizontal dimensions). A student held the metre stick in place, standing so that their shadow didn’t block the shadow of the metre stick.

We then set the compass down beside the base of the metre stick, and used the protractor to measure the angle difference in the horizontal plane of the concrete between compass north and the shadow of the metre stick. This was our ‘azimuth’ measurement.


Figure 5: Protractor (or clinometer in this case) is laid horizontally and a metre stick held vertically so its shadow passes through the origin of the protractor. A compass is used to align the base with either the north-south or east-west compass point.

My colleague in Arkansas used a simpler method for the azimuth measurement, using an iPhone compass oriented over the shadow to determine the angle from north.

Observations and Analysis
These two angles provide a coordinate for the position of the sun in the sky from the observer’s perspective. Since Little Rock, Arkansas is 1500 km from Oakville, Ontario, one would expect the sun to be in different positions in the sky from these two perspectives. We need to determine how the sun’s position in the sky is different between these two locations at the same time, but the analysis is a bit more complicated than it was for Eratosthenes as neither of our locations had the sun directly overhead (casting no shadow).

Once the two sets of angular coordinates were known, I made an assumption that might introduce a small error that will be hard to quantify. We are talking about spherical angle changes, but I treated them as planar (x,y). Under this assumption, I used the Pythagorean Theorem to calculate the ‘straight line’ angular distance between the two coordinate points. This will probably yield different results than allowing for the spherical coordinates, but I haven’t been able to work out how much.


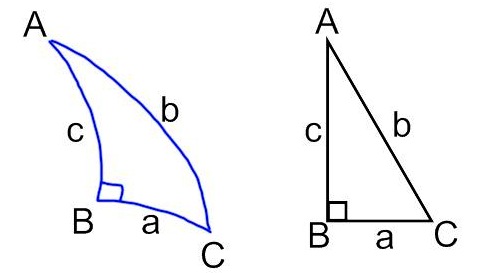Figure 6: Pythagorean theorem on spherical surface vs. flat plane.

This angle can be taken to be the same as the angle between the two locations on the Great Circle that joins them (Figures 7 and 8). Thus, the angle represents the fraction of the 360o that would take us around the circumference of Earth. So, dividing 360° by the calculated angle, then multiplying by the linear distance, should yield the circumference of Earth.


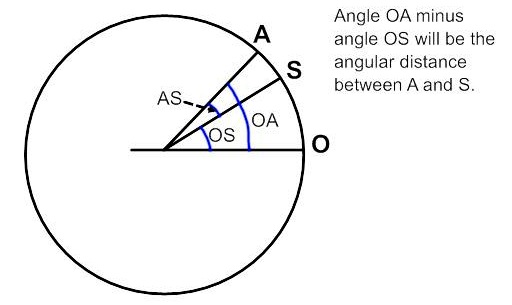Figure 7: angular measurements on a Great Circle.


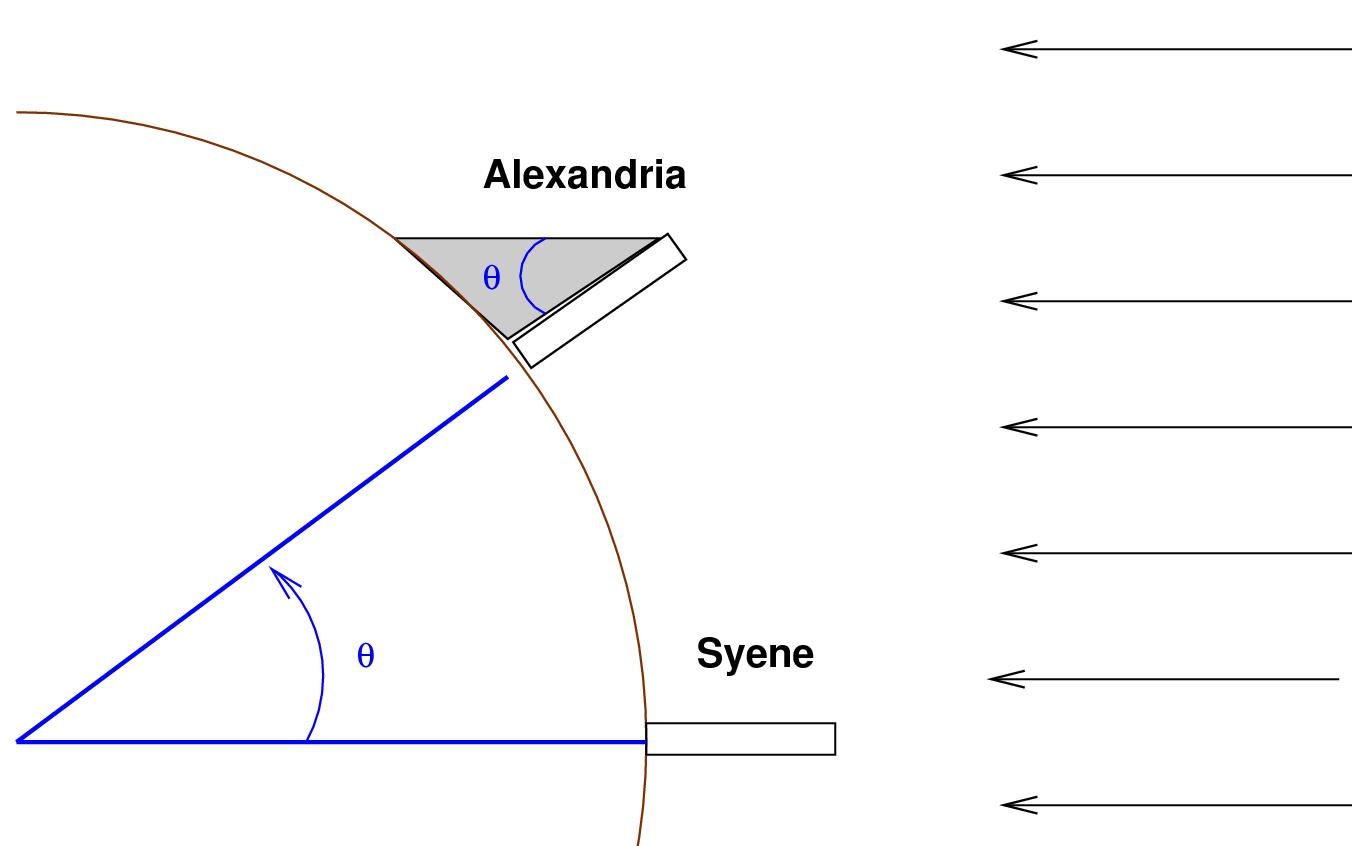Figure 8: How the two angles are related. Image @Michael Richmond, used under a Creative Commons BY-NC-SA 2.0 license.

Figure 9 shows how I used the two sets of measurements to determine the angular difference. The Little Rock coordinates were (azimuth/altitude) 81° by 67°. The Oakville coordinates were 90° by 56°.


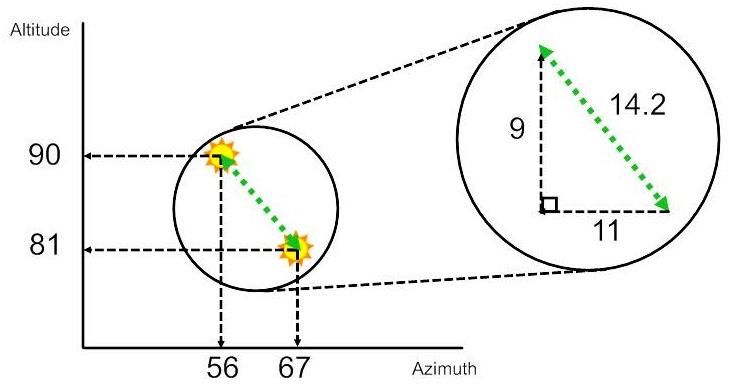Figure 9: Calculation method for determining angular distance between the two measurement locations

Using the Pythagorean Theorem, 92 + 112 = 202 and the square root of this is ~14.2. Allowing for my assumptions, this gives us an angular difference of 14.2° (Eratosthenes’ measurement was about 7°).

360/14.2 is 25.3, which means the distance between our two cities is 1/25.3 of Earth’s circumference. Thus, 25.3 × 1500 km (the distance between the two locations) yields a circumference of 38 000 km (Figure 10). Earth’s accepted measured circumference is 40 075 km, for an error of 5% in our experiment.


Figure 10: Using the angle measured and surface distance between the two points to calculate Earth's circumference

Not bad for a hacked together, rushed (we waited until we knew it would be sunny… and got distracted by our math class… and hurried to get the measurement quickly to avoid error due to the sun’s motion in the sky…) experiment by a group of academically struggling teens…

Modifications for grade 12 Earth and Space science class
I intend to redo this experiment with my grade 12 Earth and Space science class. However, these students will be asked to design the experiment themselves. Ideally, they would even find a willing partner class far enough away to aid in the precision of the measurement, but I expect that part will be up to me. Fortunately, there seem to be more mad scientists out there like me, and some of them are even crazy enough to teach. If you’re one of them, get in touch!

Tags: Astronomy, Light