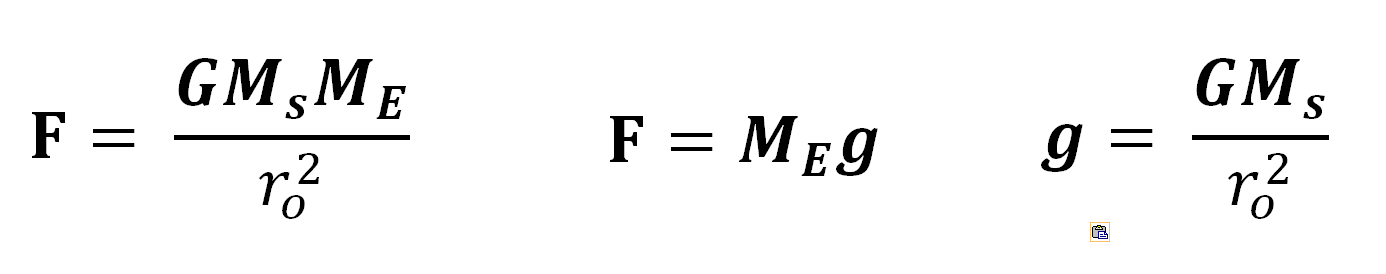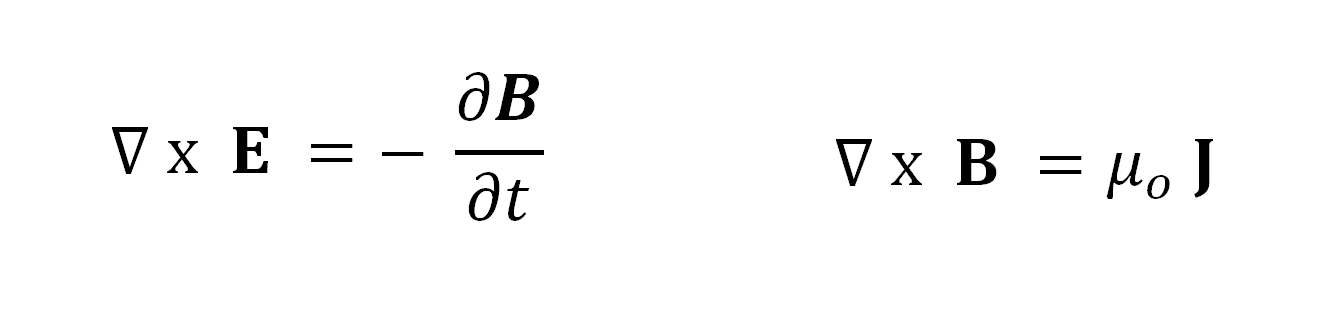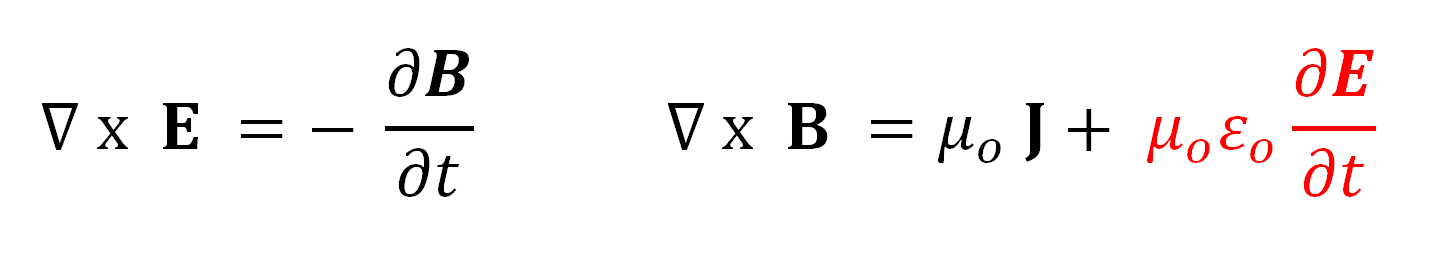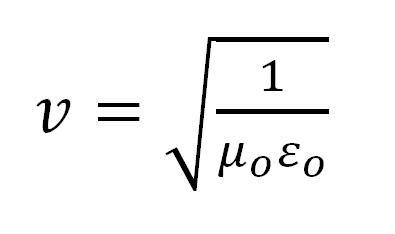Roberta Tevlin
Teacher at Danforth CTI, Manager OAPT Newsletter

The concept of fields is fundamental to our modern understanding of physics and the Ontario curriculum dedicates one of the five units in 12U physics to Gravitational, Electric and Magnetic Fields. I have struggled for many years to find ways to make this important but abstract concept more tangible to my students. Here is what I have come up with so far.

The Problem with Newton’s Law of Gravity
Newton came up with his Universal Law of Gravity by combining calculus (which he developed), equations for circular motion (which he developed) and a measurement of g within 25% (which he did). His Universal Law of Gravity was extremely successful. It unified the physics of the Earth with that of the Heavens, led the way to the discovery of new planets, and explained tides and comets. However, it has a fundamental flaw of which he was well aware. In 1693 he wrote

That gravity should be innate, inherent, and essential to matter, so that one body may act upon another at a distance through a vacuum, without the mediation of anything else, by and through which their action and force may be conveyed from one to another, is to me so great an absurdity that I believe no man who has in philosophical matters a competent faculty of thinking can ever fall into it.

https://www.sophiararebooks.com/pages/books/3537/sir-isaac-newton/four-letters-to-doctor-bentley

The math of his equation worked, but he had no idea how the force could be transmitted. The concept of fields was developed to remove this quandary. Here is how it explains the force of the Sun on the Earth, as expressed in three different formats.

Words: The Sun’s mass creates a gravitational field around itself that extends out to the edges of the universe. The Earth’s mass is in contact with this field and the result of this interaction is the gravitational force.

Mathematics: Newton’s equation, on the left, is broken into the other two equations.


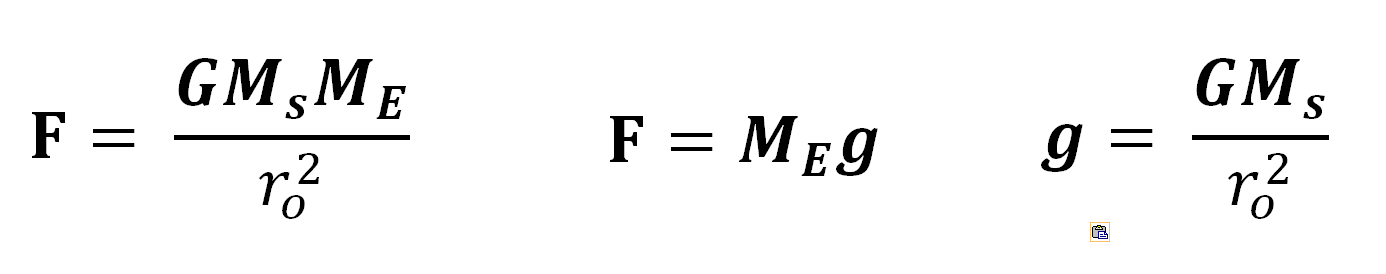Diagrams: The diagram on the left is replaced by the one on the right.


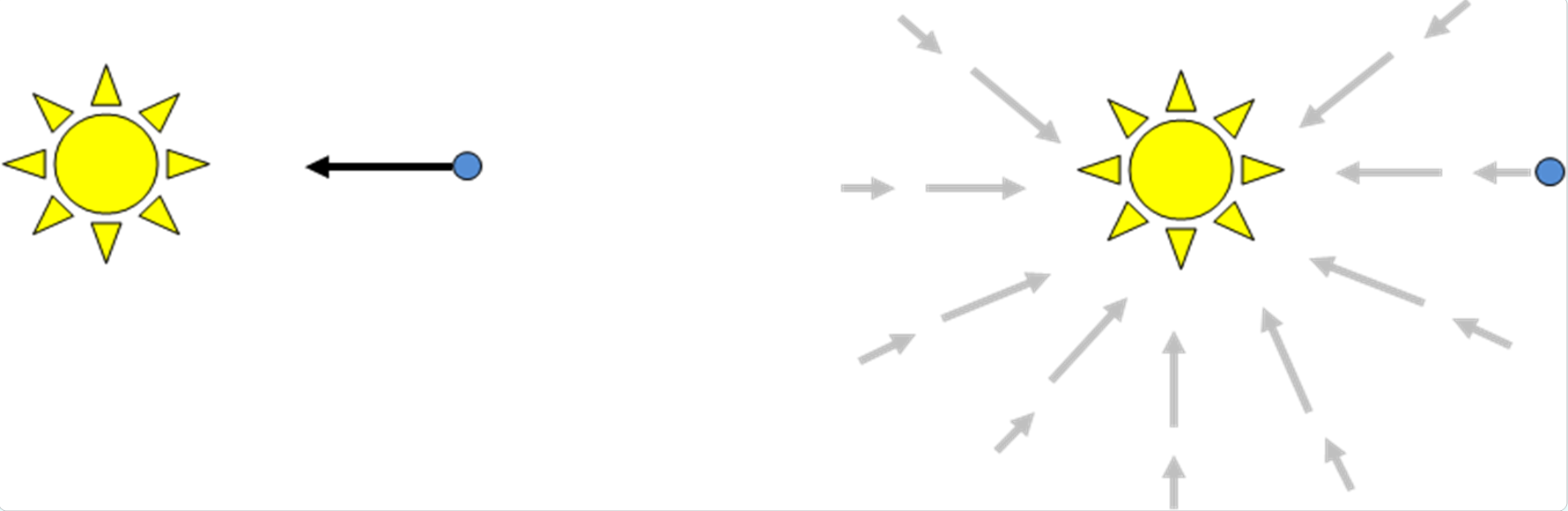
I find this very unsatisfying. It looks like we have just replaced one mystery with another one that is equally inexplicable. How do masses create gravitational fields that extend to infinity? Let’s accept this hypothesis for the moment and see if we can find support for it.

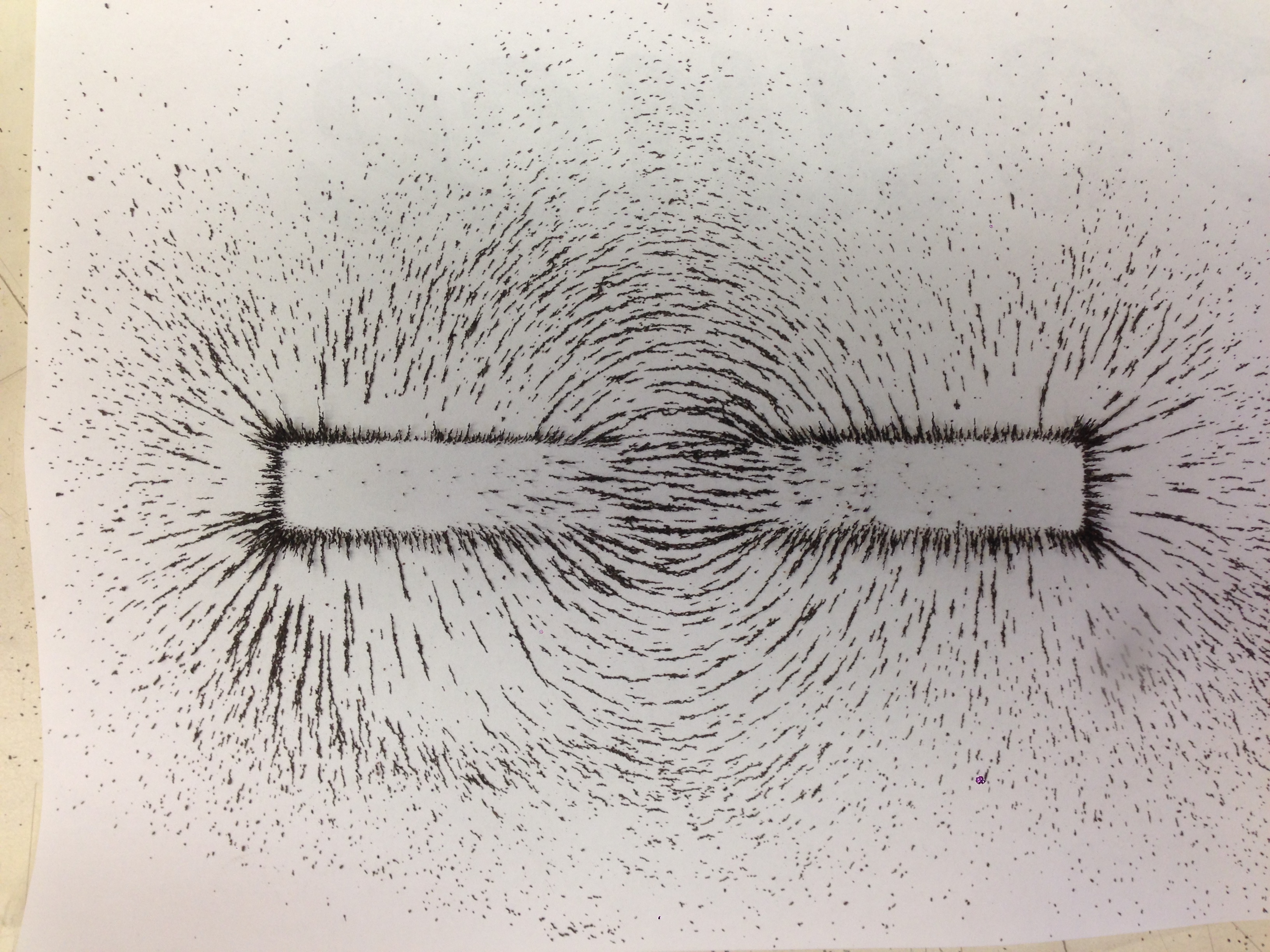
Visualizing Fields: Seeing is Believing
The problem of forces acting at a distance also applies to magnetic fields and electric fields. Magnetic fields are easier to make illustrate, so it makes sense to start with them when teaching the fields unit. I have the students do some predicting and observing using bar magnets and iron filings. The first thing they notice is that the field of a bar magnet is not as simple as the diagrams in the textbook. The field lines do not all come out the ends and there are field lines inside the bar magnet as well as outside.



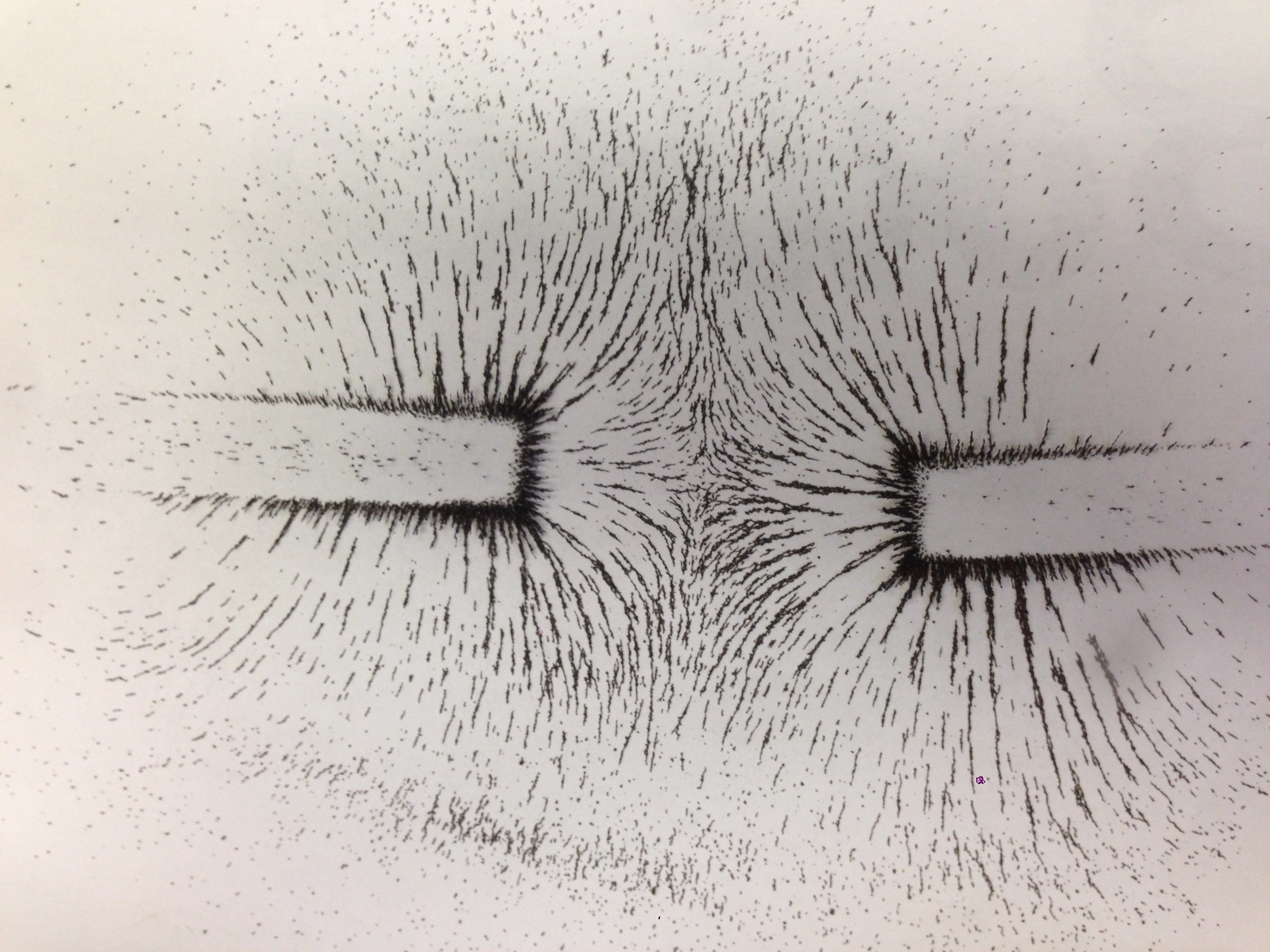
What will the field will look like in between the poles of two magnets? This challenging question involves vector addition without using numbers and is made easier by considering symmetry. Opposite poles give a very different pattern from two identical poles.



Next I challenge the students to use balloons to show electric fields with similar patterns.



The field around a planet will be similar to the field around a charge. What will the field between two planets look like? Will it be similar to two opposite poles because the planets attract each other? Will it be similar to two identical poles because the two planets are the same? This one is tricky. Consider what you will feel if you are placed halfway between these two planets. You will be pulled in opposite directions by equal forces - a net force and therefore a net field of zero. This matches the field pattern of the identical poles.

Modelling Fields with Fabric
Stretchy fabric lets you model how fields make objects move. It shows how circular motion results from an inward force and a tangential velocity. It shows that larger orbits have a longer year, that a ball launched too fast will escape and that any dissipative forces will cause the object to spiral in.

There are two different ways to support the fabric. You can either have a group of students holding the fabric edges or you can support the fabric on a large ring, like a bicycle wheel. The first version gives students a better feel for the physics, while the second one is able to show many more stable orbits.



The fabric can also be used to show the effects of a repulsive field; you just need to pull UP on the centre instead of down. In this form it can model how a gold nucleus affects the alpha particles in Rutherford’s experiment.

Simulating Fields with PhET
Rutherford scattering can be explored more deeply using a computer simulation like https://phet.colorado.edu/en/simulation/rutherford-scattering.



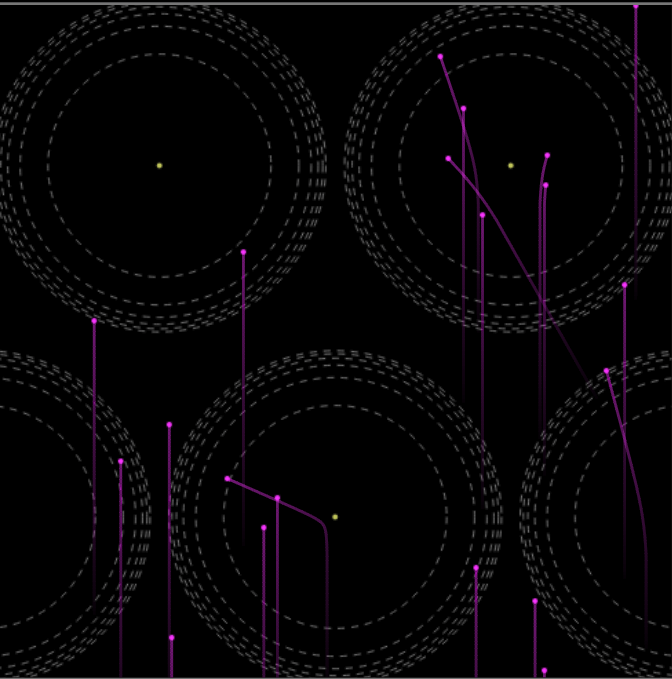
Another simulation that gives a feel for the effect of fields on motion is Electric Field Hockey. In this game, you add charges to produce a field that will guide the charged puck into the net.



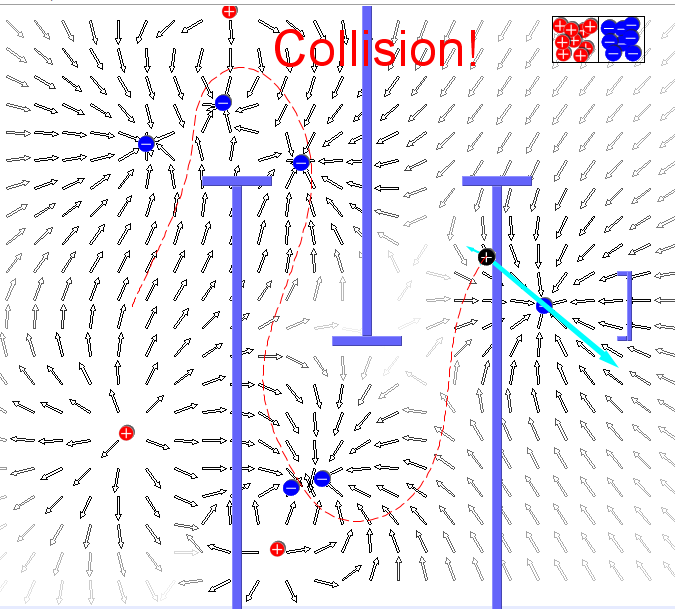Applications of Electric and Magnetic Fields: Physics in Action
In both grades 11 and 12, students explore the affect of gravitational fields. The effect of electric and magnetic fields is harder to demonstrate. Fortunately, TRIUMF has produced a very good video showing how fields are used to speed up and turn particles in cyclotrons. The video does not try to be flashy or engaging — just clear. I appreciate that. The video comes with worksheets and extra information for the teacher. This video is rather hidden in their website, but this link will take you there.



Faraday and Maxwell
Faraday introduced the concept of fields to explain electromagnetism and he produced key experimental evidence to support this idea. Maxwell took Faraday’s work and that of others and unified them in four equations. Maxwell’s Laws are mathematically beyond the scope of grade 12 physics students but a brief conceptual introduction to them can be useful.

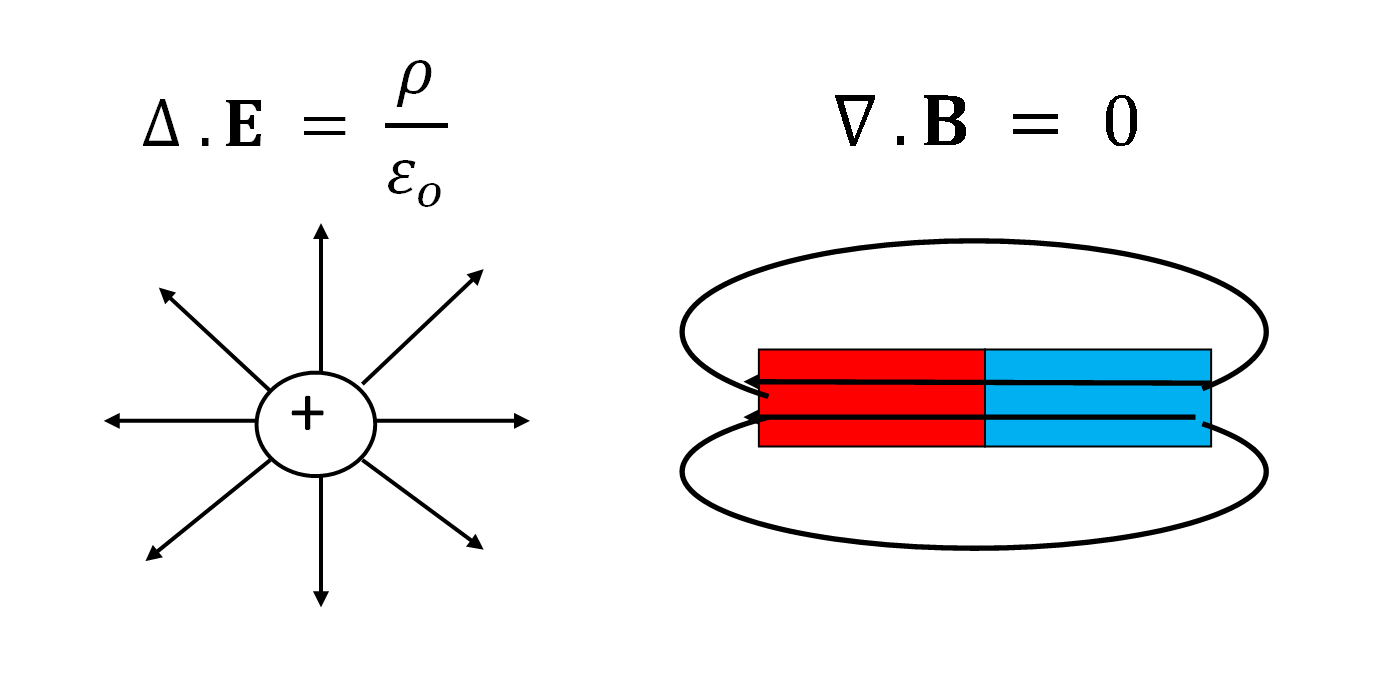
The diagrams below show the fundamental difference between electric and magnetic fields. Electric field lines radiate from charges but magnetic field lines always form loops. The equations say the same thing, but in a mathematical form. The first law describes how the electric field comes from the charge density, ρ, divided by the electric constant, ε_o = 8.854 × 10^-12 A²s⁴/m³kg. The second law has a zero on the right because there are no magnetic monopoles; the poles always come in pairs.



The third and fourth equations show the other ways to produce electric and magnetic fields.



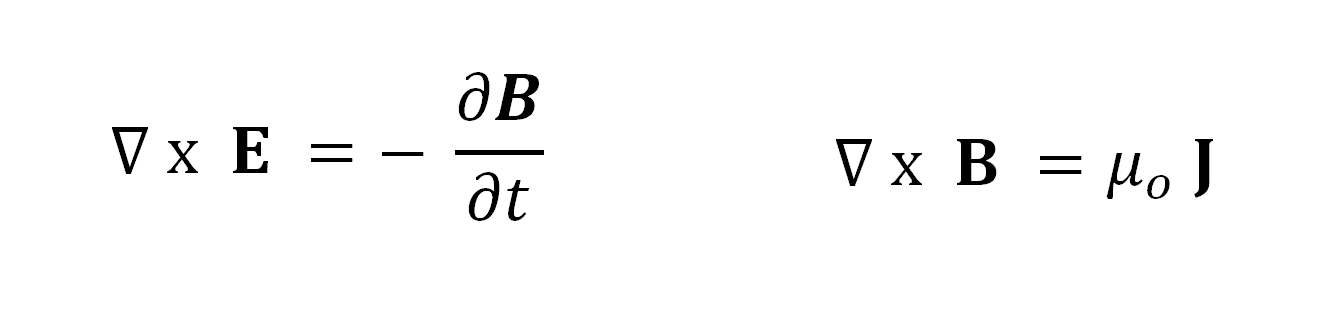
The equation on the left says that a changing magnetic field will induce an electric field. This is the basis of electrical generators and transformers. The equation on the right shows that a magnetic field results from a current density, J, multiplied by the magnetic constant μ_ο = 1.257 × 10^-6 m kg/s² A². This is the basis of electromagnets and motors.

Maxwell wasn’t satisfied with the symmetry of the last two equations. If a changing magnetic field could cause an electric field, then he felt that the reverse should also be true. He added another term.



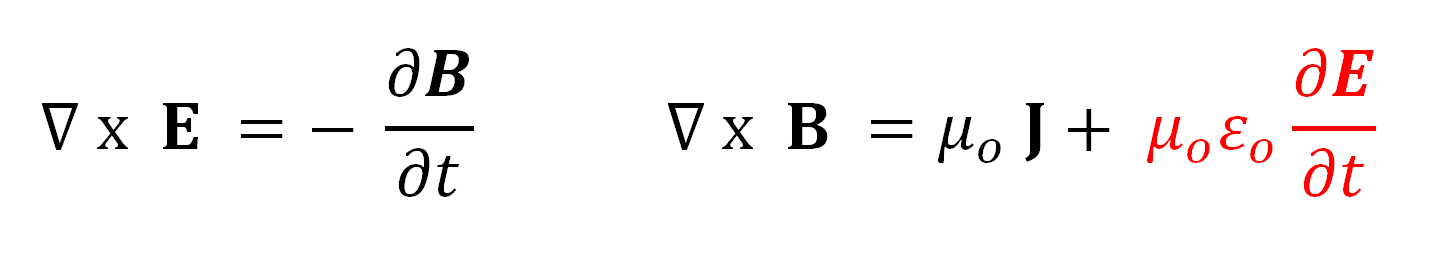
This extra term means that a changing electric field can induce a magnetic field that in turn induces an electric field, and so on. Maxwell predicted that this disturbance in the field will propagate at speed given by



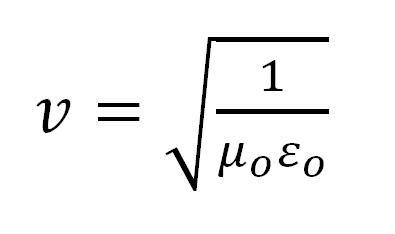
I ask my students to calculate this speed and they are always surprised that it is the speed of light. They learned about electromagnetic radiation in grade nine science (astronomy unit) and in grade ten science (optics unit), and yet they are still surprised. The PhET simulation radio waves helps to see how these EM waves are generated.



The ideas discussed so far are summarized in Minute Physics: Real World Telekinesis


The video also introduces the idea that fields are central to modern physics.

Modern Physics and Fields
Maxwell’s equations predict the speed of light without specifying a reference frame. Einstein decided that this means that the speed of light does not depend on which reference frame you use; the speed of light is invariant. Einstein put this invariance and Galilean relativity together and came up with special relativity. From this we get nuclear power, PET scans, and a host of other modern technologies.

Ten years later, Einstein added gravity to his theory of relativity. He suggested that gravity is a fictitious force — a result of the curvature of spacetime. Masses curve spacetime and this curved spacetime tells masses how to move. This extension brought us black holes, gravitational lensing, gravitational waves, and the GPS.

Special and general relativity extended the concept of fields. However, quantum physics alters the field model dramatically. It explains what a field is made of: it isn’t something smooth and continuous. Fields result from the exchange of virtual particles. A virtual particle comes from nothing and violates the law of conservation of energy. However, they do this so fast that the Heisenberg Uncertainty Principal is able to ensure that this theft is never discovered. A vacuum is not empty, but full of virtual particles appearing and disappearing. If a virtual particle interacts with a real particle, it shows up as a force.

The repulsion of like charges can be explained by the following diagram. One charge emits a virtual photon and moves in the opposite direction to conserve momentum. The virtual photon is captured by another charge, which must move to conserve momentum.



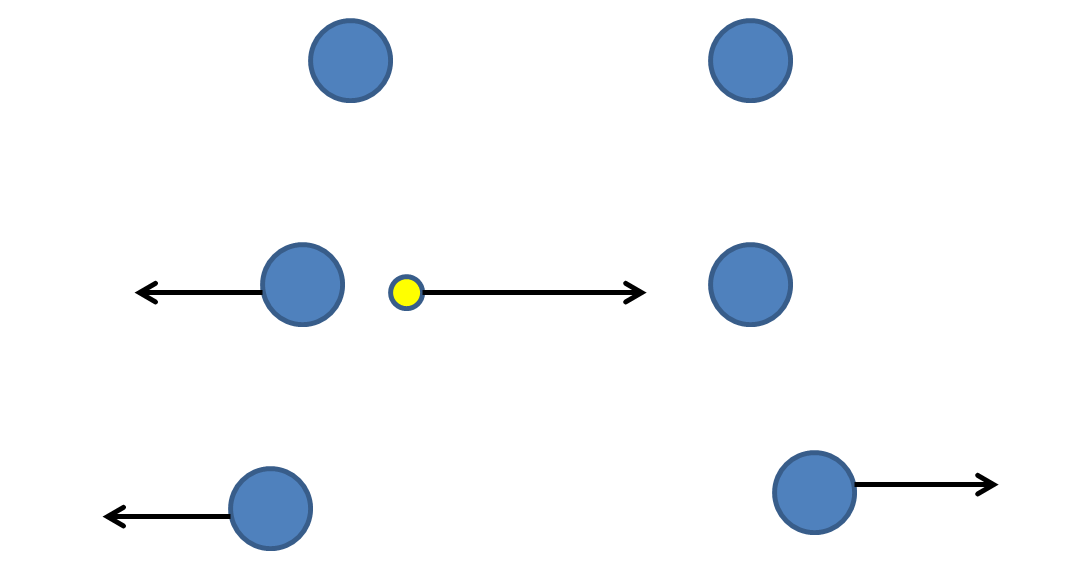
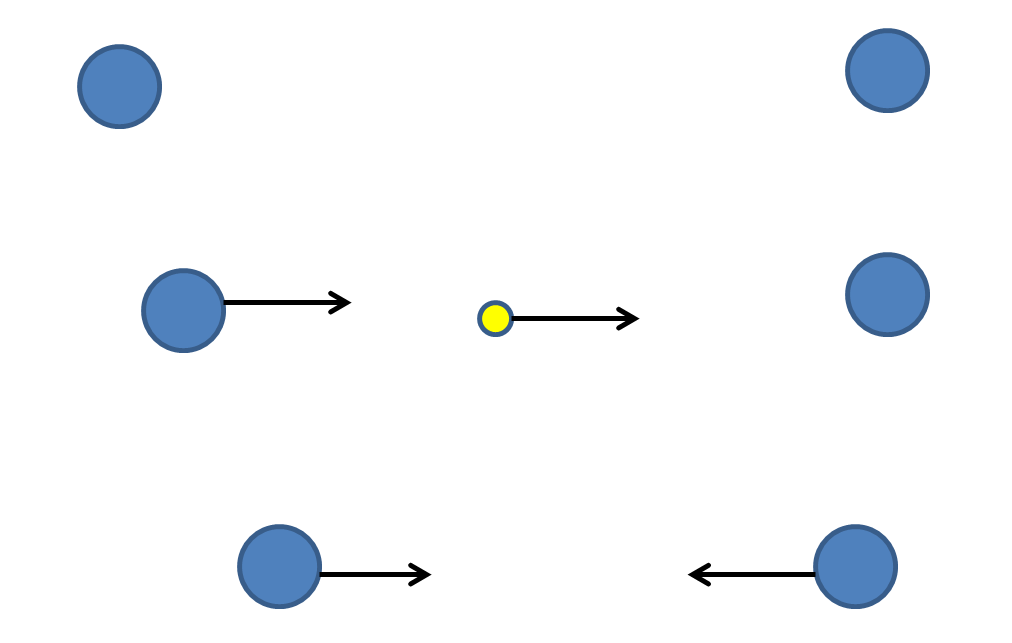
Attraction is harder to imagine, but can be described as the same process with the photon carrying backwards momentum (or forward momentum backwards in time).



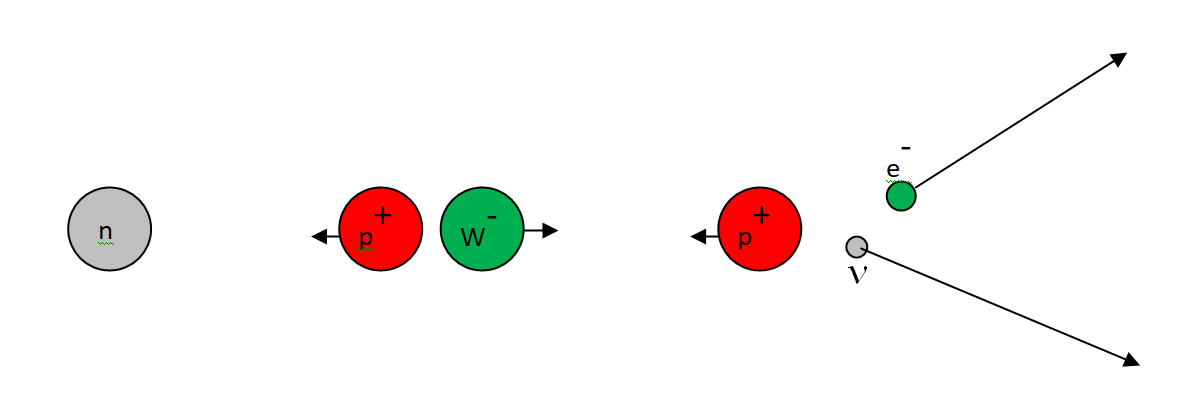
The strong nuclear force holds the nucleus together by the exchange of virtual gluons. The weak nuclear force does not involve any pushing or pulling. It determines how particles decay and it does so by the exchange of virtual W and Z bosons. For example, beta decay involves a neutron turning into a proton, neutrino and an electron by the exchange of a W^– particle. The W^– particle ensures that charge is conserved. When it is emitted, the neutron become a proton. When it decays, the charge is carried off by the electron.



The final exchange particle is the one that gives particles mass — the Higgs boson. Finding the Higgs boson was evidence for the Higgs field which had been proposed almost half a century earlier. This short video does a nice job explaining how the Higgs field can give rise to a Higgs boson.



Editor’s Note:
Roberta will be presenting this material at the OAPT Conference on Saturday May 12 at 9:00 AM.

Tags: Electricity, Field Theory, Magnetism, Modern Physics