Chris Meyer, York Mills C. I., Toronto
Christopher.meyer@tdsb.on.ca

The Gold Medal Race
It was a thrill to watch the Toronto high school student Penny Oleksiak win gold in the pool at the Rio summer Olympics. Now my students and I watch her win every semester as part of our new motion unit for grade 11 physics. In this article, I will describe the new pedagogical ideas that I have built into this unit, starting with Penny Oleksiak. Penny’s outstanding performance is a great example for physics students because: she’s awesome, she’s female, she’s still in high school, and it draws students into a real application of what they learn: sport science.



Sports Data
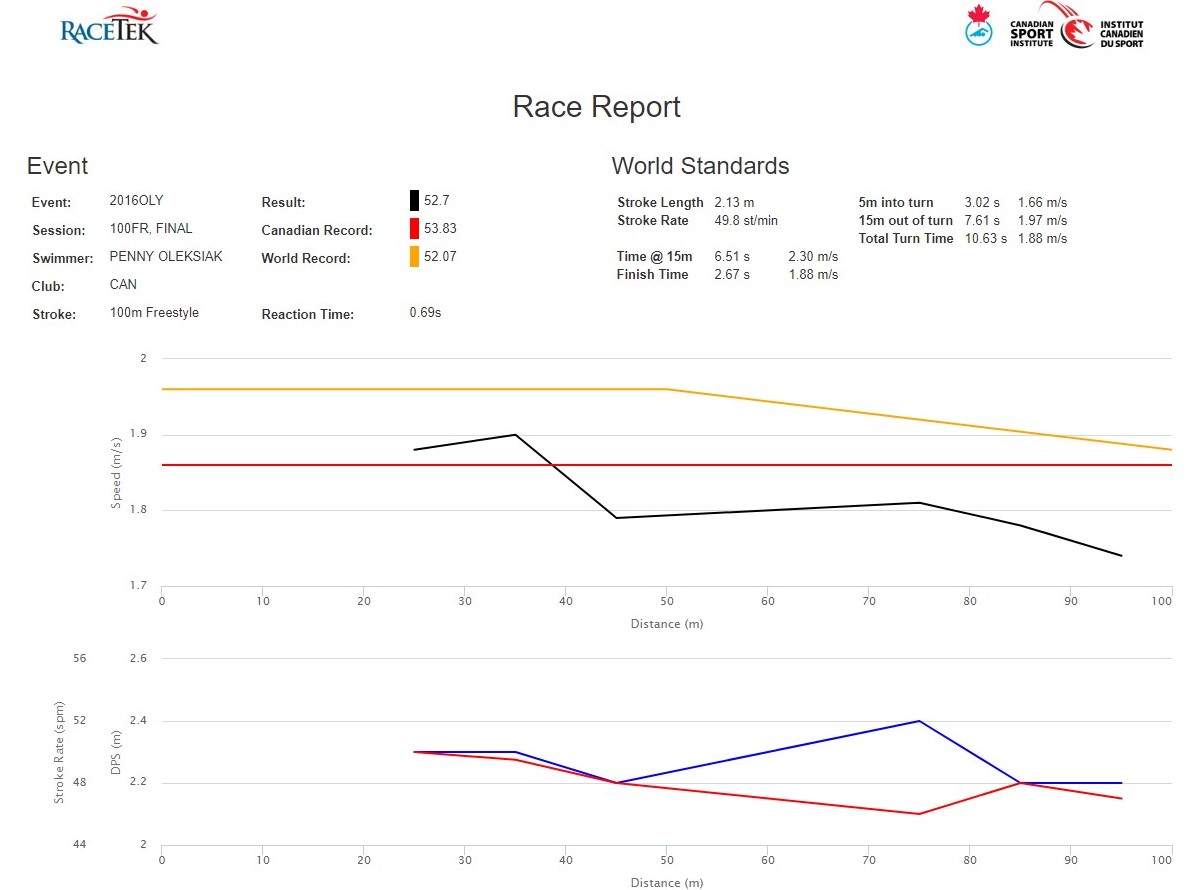
I reached out to Ryan Atkison of the Canadian Sport Institute, who was one of the scientists working with Penny as part of her Olympic training. Ryan was most obliging and has kindly given permission to share the data and video footage from Penny’s gold medal race. The race data is woven through the whole motion unit and we return to it many times using different approaches as students’ understanding grows and develops. There is a lot of interesting information in their data set, but we focus on the position and velocity data.



A Course Introduction and Motion Unit
Time for a bit of background on the course itself. Our grade 11 physics course is inquiry-based and does not involve traditional lectures. Students work in cooperative groups and explore physics ideas by following guided-inquiry investigations. The first few lessons train students to work productively in this learning environment: how to work effectively in groups, how to answer written questions thoughtfully, and how to think about, write, and use numbers. Then, they are introduced to Penny!

How Do Scientists Study the World?
The first time I showed my students the video of Penny’s race, I asked them to watch and describe Penny’s motion. I was excited because the race is a really good example of constant velocity, but the students were having none of that. They described how her arms moved, her kicking motion, her push off the wall, her breathing: everything except what I wanted! They were drawn to each interesting tree and studied each leaf, without seeing the forest. Scientists quickly look past such distracting features and home in on the core physical ideas. In the process, scientists create simplified mental pictures, or models, of physical phenomena that allow them to work productively with a very complex world. You and I do this almost instinctively, but students need explicit training in this vital skill.

Start Your Modelling Career
Modelling is a core physics skill that is seldom explicitly addressed. In fact, it is a skill that I was unaware of for many, many years despite using it almost daily¹. All physical phenomena are too complex to completely describe. Instead, we create models, simplified mental pictures with simple rules, whose behaviour bears some resemblance to what we observe. Models are not arcane abstractions better left for advanced studies, they are fundamental to what you and I do every day in our classes. If you help your students learn about models, their physical reasoning will become more sophisticated and you will find yourself with helpful tools to deal with many thorny teaching situations. It’s never too early to start one’s modelling career!

Assumptions: Looking Past the Trees
Models start with assumptions: simplifications that we know are wrong! Assume friction is zero. Assume the object behaves like a point particle. Assume energy transfers occur without loss to thermal energy. How do we get away with saying such crazy things? The power or utility of any model lies in its ability to explain and predict; this is why scientists use them. If a model gives predictions that are a close match to certain aspects of the real physical phenomena, we no longer think of these assumptions as “wrong”, instead we think of them as reliable under certain conditions. The assumption that friction is zero is likely reliable if the size of the force of friction is fairly small compared with the other forces. When we talk about models and assumptions this way, we provide tools for our students to make their own reasonable assumptions and to begin looking past the trees in search of the forest.

Taking it to the Limit
Another defining characteristic of a model is a range of validity. A good model describes certain phenomena really well inside this range, but can fail spectacularly outside of it. Quantum works great for small things, general relativity for big or dense things, and Newton’s Laws covers the mushy middle. In my classes, the most common range is an interval of time. We can create a model of a free-falling object by assuming that air resistance is zero. This model can fail because the force of air resistance is no longer small compared with the force of gravity. But it will also fail when the object makes contact with a hand. This helps explain why we cannot use a final velocity of zero to describe the object’s motion: as soon as it contacts the hand, the forces, and model, change. All good models have limits. The example below shows a solution for recent grade 11 forces test, completed by my colleague. In it you can see how we represent the models and provide structure for students to carefully work with the different intervals of time. This is a challenge for students, but the scaffolding you see on this test helps them organize their ideas and show their understanding.



Improving Your Models
Have you ever watched an experienced physicist tackle a very novel problem or situation? A common starting point is to create an absurdly simple model that has just the barest of features in common with the actual phenomena. Hence the classic physicist and cow joke (punchline spoiler alert: assume a spherical cow in vacuum). The absurdly simple would be comical if it was the end point in the modeling process. However, scientists work with models in an iterative way, refining or relaxing assumptions in pursuit of higher quality predictions or a greater range of reliability. And improved models save lives! This past fall, when our grade 11s were being introduced to models, scientists at the National Oceanic and Atmospheric Administration (NOAA) were frantically revising models to predict the path of some of the most devastating hurricanes in recent memory.



Testing Your Models
Having the language of models allows students better reasoning tools when they test predictions. When a measurement disagrees with a prediction, we look for reasons why. Sometimes the difference comes from statistical variations in the measurements, but other times it has to do with the quality of the assumptions built in to the model. Consider the acceleration of a cart along an incline from grade 12. Now I have conversations with students more like this:

“What does your model assume about this situation?”

“That … the…friction is zero.”

“Since there actually is a small amount of friction, should your model's prediction be higher or lower than the measurement?”

“Umm… it should be a bit higher”

“Is that what you observed?”

“Yes.”

“If you wanted to improve your model, what else could you measure about the system?”

“I could measure the amount of friction.”

Consider how far we have come from a traditional plug and chug question to find the acceleration. All of this begins on day 4 of grade 11 physics when we meet Penny.

Off to the Races
Time to analyze Penny’s race! The first motion lesson introduces students to the core ideas of modelling: making assumptions and identifying the interval of time during which the model is most reliable.

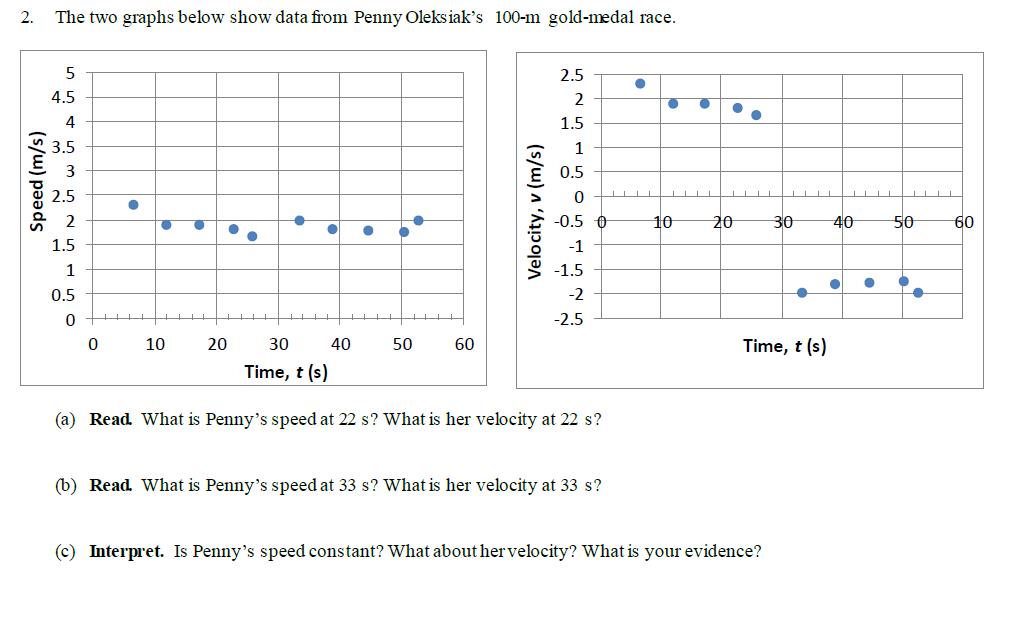
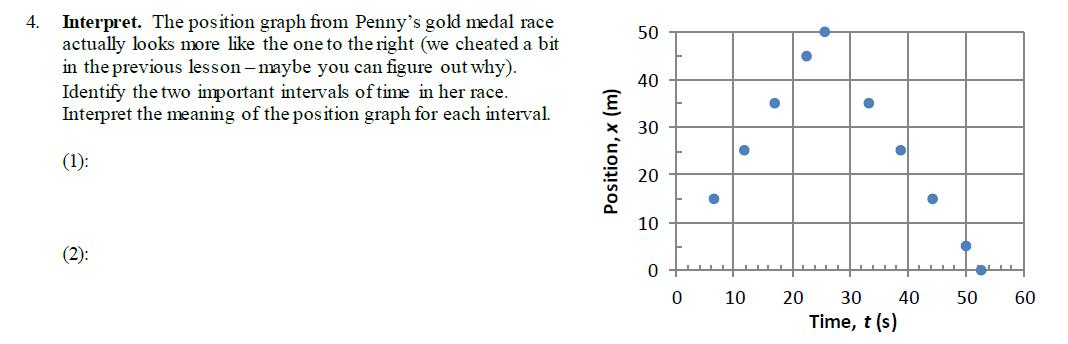
As we continue through the motion unit, we return to the race data and examine it through the lens of new physics ideas, like position graphs:


speed or velocity graphs:


Events and Intervals
I can’t believe that I taught physics for 10 years without having clear vocabulary to describe when our models and our interest in a situation start and end. It took a new approach to my grade 12 unit on special relativity to remind me how important the idea of an event was to all of physics. An event is something that happens at a certain position and time: the runner reaches the 50-m mark, the collision begins, the ball leaves contact with the hand, or the spring is released. A starting and ending event define an interval of time or space (displacement). Many difficulties learning physics stem from mistaking short intervals as single events. Students will often describe the event "she catches the ball", which usually leads to confusion. Are we interested in the moment in time when the ball makes contact with her hand, or the moment when the ball comes to rest? This makes a big difference. Catching a ball is a process that requires an interval of time and is bookended by two very different events. Take another look at the freefall and catch test question shown above. In this unit on motion, events and intervals are introduced by lesson 4 and are used consistently through the end of grade 12.


How Do You Think You're Doing?
One reason students produce shoddy work is that they don't reflect on its quality and identify what can be improved. This skill is an aspect of metacognition: the ability to monitor the quality of one's own thinking and work; and the ability to identify when change, improvement, review, or extra learning is required. High-performing students and "life-long" learners do this regularly, almost instinctively. Students need to practice this skill so that it becomes part of their regular working and thinking habits. We train our students how to carefully write responses to questions, but this is not enough. They need regular opportunities to reflect on their work, compare it with good quality examples, and make corrections and improvements. We do this by choosing one question from each investigation and asking students to come to the front of the class to compare their work against a model answer. When students look at high-quality work, there are times when they do not recognize what features in it are important. To assist with this, we include commentary along with the model answer that helps remind students of the characteristics of high quality work and helps them identify the significant features of the model answer that often go unnoticed².



Deliberate Practice
There is good research³ that says that you need about 10 000 hours of practice to become an expert at something. Often overlooked in discussions of this research is what kind of practice is required. Effective practice is done thoughtfully, is carefully graduated in its level of challenge, and needs to come with immediate, targeted feedback. How often does the average student experience these conditions while doing homework? If they don’t, what is the value of that work? To help our students’ practice become more thoughtful and deliberate, we include a metacognition check at the end of their homework. Students mark their work according to a set of criteria chosen for that work. The evaluation process might have reminded them about some overlooked ideas, so they are encouraged to use a different colour pen or pencil to go over their work and make improvements. When I evaluate their homework (yes, I do) it is based on how thoughtfully they have completed their work and gone through this process, rather than whether their work is right or wrong (I still highlight any inaccuracies, but I don’t evaluate based on it — it is normal to make mistakes when learning something new).


Student, Improve Thyself
A recurring theme in this unit and course is the idea of improvement. All our work — the daily investigations in class, the homework, and the assessments — are focused on the goal of improvement. We want students to feel okay making mistakes and learning from mistake rather than dreading them. However, if there is no opportunity for genuine improvement, then all this is just lip service. If students do thoughtful, careful work to improve their understanding and skills, we offer them the opportunity to rewrite any test or quiz. Our tests are returned with an improvement page that is a mandatory piece of homework, regardless of the student’s test performance. Students are asked to reflect on their work, identify the difficulties or oversights in their work, and write corrected responses. If this is done thoughtfully and other evidence of improvement is shown, the student has the opportunity to improve (i.e. replace) that mark.


Students are mark driven: don’t oppose this, use it. Just make sure the marks are encouraging productive behaviours. One day, when their fever breaks and they wake up from their mark-driven stupor, they will hopefully discover that they have been practicing the habits and skills of the life-long learner.

Estimation Skills
Legendary physicist John Wheeler remarked, in a theoretical physicist-kind-of-way, that you should:

“Never make a calculation until you know the answer. Make an estimate before every calculation, try a simple physical argument (symmetry! invariance! conservation!) before every derivation, guess the answer to every paradox and puzzle. Courage: No one else needs to know what the guess is. Therefore make it quickly, by instinct. A right guess reinforces this instinct. A wrong guess brings the refreshment of surprise. In either case life as a spacetime expert, however long, is more fun!”— John Wheeler

from E.F. Taylor and J.A. Wheeler, Spacetime Physics (1992), 20⁴

Our students should do this too! This is great exercise for developing one’s physical intuition and common sense about the numbers involved with physics. Now, our students won’t begin with the sophistication of the person who coined the term “black hole”; they start much simpler. Training begins in the third lesson of grade 11 where students estimate simple measurements and estimate calculations based on those measurements.

Estimations become integrated into our routine problem solving process, giving students two years of regular practice with Wheeler’s advice. In grade 12, the estimation skill is enhanced with Fermi problems.

Making Sense of Math
An important challenge in learning physics is to look at equations and numbers and see physical meaning. There are many reasons why this does not routinely happen, including how the brain processes mathematical symbols and how students are trained in their math classes. This will be the focus of another article coming soon to a physics newsletter near you. The takeaway from this is that we need to provide students with opportunities to make sense of the mathematics they use. Our starting point is preventing students from vomiting mathematics onto the page. In fact, when it's time for a calculation, the first step is to describe the purpose of the mathematics they are about to use.



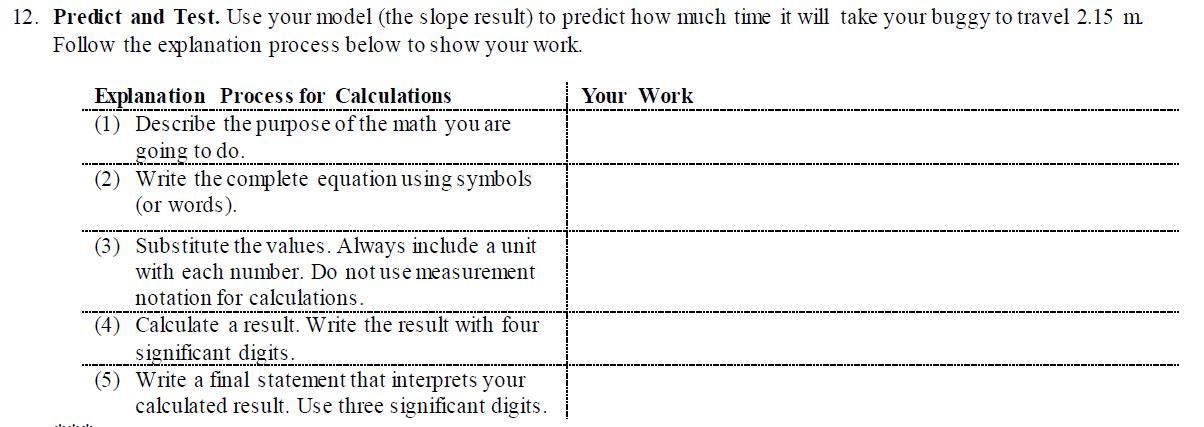
In physics, we always use mathematics with a purpose in mind, and each step in a lengthy solution will have a unique purpose that contributes to the final result and these should be described. This not only helps students clarify in their own minds the purpose of their mathematical work, it greatly increases the readability of the final product. It is now pretty rare that I have to search through a page of scribbled symbols to find the next step in a student’s solution.



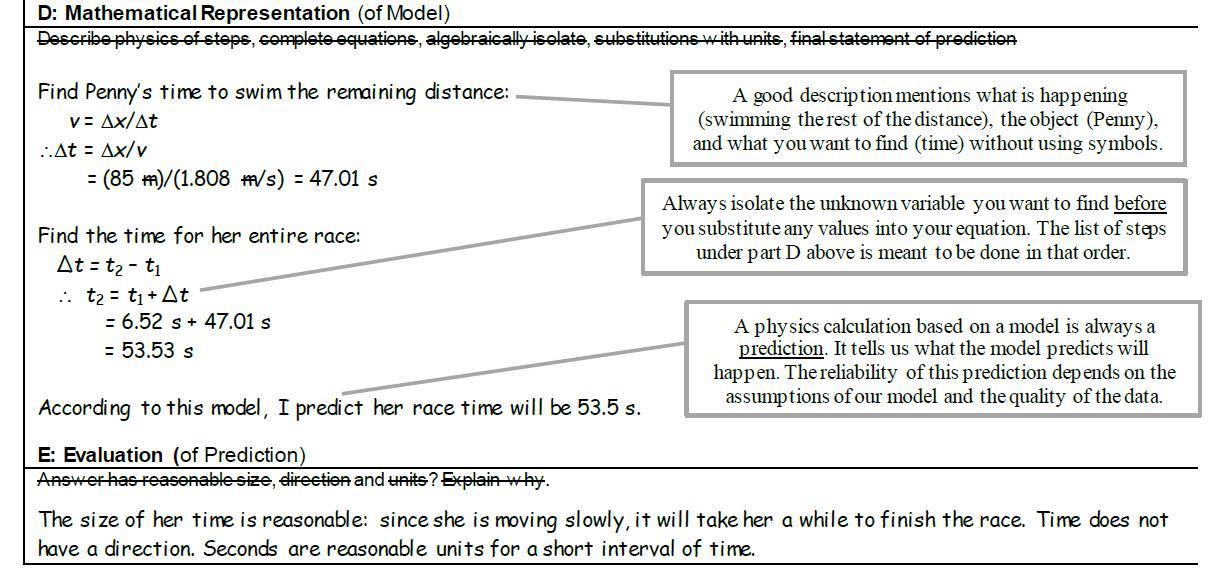Sequences of Mathematical Skills
Our math routine shown above establishes a linked sequence of skills that trains students to work in a disciplined way. The sequence is always the same: description, complete equation, algebraic isolation, substitutions, result. After the description, students write a complete equation using algebraic symbols and event numbers. For example: Δy₂₃ = v₂Δt₂₃ + ½a(Δt₂₃)², which relates the displacement between events 2 and 3 to the initial velocity at event 2 and the acceleration and time interval between the two events. This provides a clear and recognizable starting point for the reader. Next, students algebraically isolate for the quantity of interest. So, if v₂ is zero and we are interested in the time, the students isolate Δt₂₃. Notice how the event notation helps focus our attention on a specific interval of time for our model. The isolation step also helps build skills for more advanced physics work. Now we are ready to substitute values into the rearranged equation, being sure to include the units. As I mentioned in a previous article, the inclusion of units is not just window dressing, but triggers important reasoning about units and conversions. At long last, the student can now unlimber the calculator and find a result. This sequence of skills is introduced in lesson 3 of the course and is printed on every solution page to provide the very regular reminders students need to avoid vomiting math on a page.

Make Your Predictions
Computing a numerical result is not the end of our problem solving work. Students must state their result as a prediction. This is the icing on our modelling cake. “I predict the acceleration of the cart up the incline will be 1.63 m/s²”. Grade 12s include an uncertainty with their prediction. This description as a prediction might seem pedantic, but it emphasizes an important shift in understanding. All our physics calculations are based on models whether we acknowledge this or not. Models can only explain or predict. I realized how important this change in language was when a student asked me: “why do we call it a prediction? Once we calculate it, isn't it real?” Ah, the epistemological joy! The answer to that question is an emphatic “no”! Ask most students what a prediction is and they will tell you it is a kind of guess about what will happen in some situation. To a scientist, a prediction is a logical deduction about the outcome of an experiment or a situation based on some assumed set of principles or model. We only ever hope our predicted results to be “close” to some ideal measurement of the system. The model is not the system.

Does the result make sense? Is the model reliable?
Students need to consider whether a calculated result seems reasonable, or if their might be a problem with their work or model. We employ one final sense-making step to check whether the size, direction, and units of the final result seem right. Ideally, we would like students to compare the result with some known information, deciding that, for example, 64 km/h is a reasonable speed for a car on a city street. Once all that is done, if we can, we have students test their predictions with a measurement. In science, the arbiter of “being right” is not a teacher: it is nature and our measurements of her.

Bridging the Math and Physics Divide
In an earlier article, I described some of the challenges when using mathematics in the physics classroom. Mathematicians and physicists both “speak math”, but we use different dialects. Students need to learn how to translate from the math they speak in math class to the math we speak in a physics class. An important part of this is the use of symbols. There are many ways in which physicists use symbols differently than mathematicians (which will be detailed in a future article!). One difference is context: we change our symbols depending on the phenomena we study. For example, in math class, slope is almost always written using m, x, and y. In physics, the choice of letter for our symbols is important since it assists with our interpretations of the quantity’s meaning. Students need to practice changing from math symbols to physics symbols, such as in the example below.

The Final Pieces
The purpose of this article was to introduce and explain some of the more recent changes I have made to my teaching of motion. There are lots of other interesting details about the design of this unit that you will have to discover for yourself! Download it (link to the resources section of the article) and read it through. Even better, complete the questions and try out some of the new skills yourself. An important part of this unit is a series of short brain lessons (link to the resource section of the article) that help students understand how their brains learn and to address some of the traditional challenges of learning. A particularly important lesson is “Diversity in Thinking” that encourages girls to pursue physics. These lessons will be the focus of a future article and are still a work in progress, but I feel they already form an important part of the grade 11 physics course and wanted to include them here.

Resources
There are many resources that go together to create our grade 11 physics course. You can download some of these files here:

• The New Introduction and Motion Unit (http://www.meyercreations.com/physics/resources/New%20motion/11%20Handbook%20-%201%20Motion.pdf)
• A New Force Unit that continues the modeling theme (www.meyercreations.com/physics/resources/New%20motion/11%20Handbook%20-%202%20Forces.pdf)
• Sample Answers for student self-evaluation (www.meyercreations.com/physics/resources/New%20motion/11%20Handbook%20-%20Self-Eval%20Exemplars.pdf)
• Brain Lessons (www.meyercreations.com/physics/resources/New%20motion/Brain%20Lessons.pptx)
• Course Guides (http://www.meyercreations.com/physics/resources/New%20motion/Course%20Guides.zip)
  
  

Invitation
If you would like to see any of these lessons in action, please email me and we can set up a time for you to visit. My door is always open.

Notes

1. I learned about it from the work of Eugenia Etkina, for example: https://drive.google.com/file/d/0By53x8SYAF1lRVdJcnZiSVNYaXM/view
2. Thanks to Roberta Tevlin for the 4C’s idea for assessing written responses.
3. Ericsson, K. Anders, Ralf T. Krampe, and Clemens Tesch-Römer. "The role of deliberate practice in the acquisition of expert performance." Psychological review 100.3 (1993): 363.
4. Thanks to David Harrison at U of T for highlighting the importance of Wheeler’s suggestions.

Tags: Motion, Pedagogy