Chris Meyer, OAPT VP teaching and learning, Assistant curriculum leader York Mills C. I.
Christopher.meyer@tdsb.on.ca

A model educator
In science, we create models to help us explain our universe and predict what might happen next. Science is a continuous process of creating, expanding, testing and revising models, which are judged by scientists according to their agreement with observations. As educators, we should choose models that have a reasonable agreement with observations, are conceptually clear, and do not create unnecessary hurdles to future, more sophisticated, models. This task is especially challenging with the topic of energy, a concept that is fundamental to physics and all branches of science. Research into the pedagogy of energy has shown that traditional treatments of energy leave much to be desired. A growing consensus is forming around a quasi-material model of energy¹, where we think of energy almost like a material object. But don't panic! This is not a return of the old caloric model in disguise. Interestingly, this approach was anticipated by Richard Feynman in his story of the mischievous boy Dennis and his toy blocks. I’ll leave it to Richard to introduce this approach to energy:

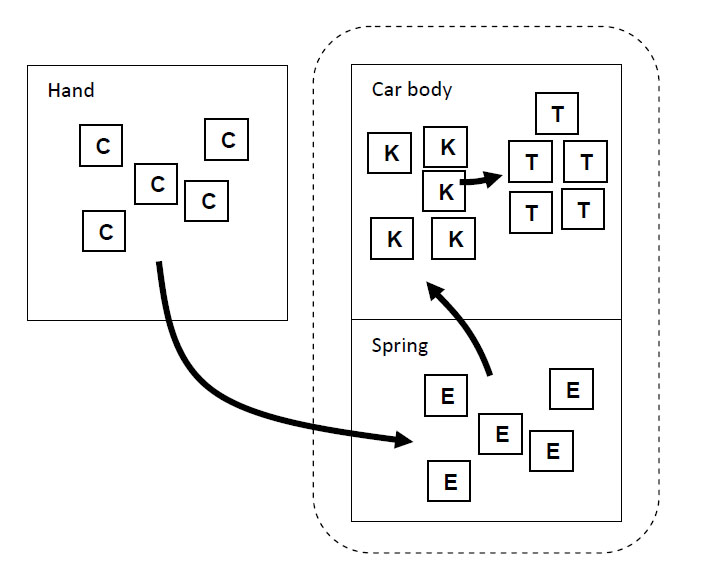
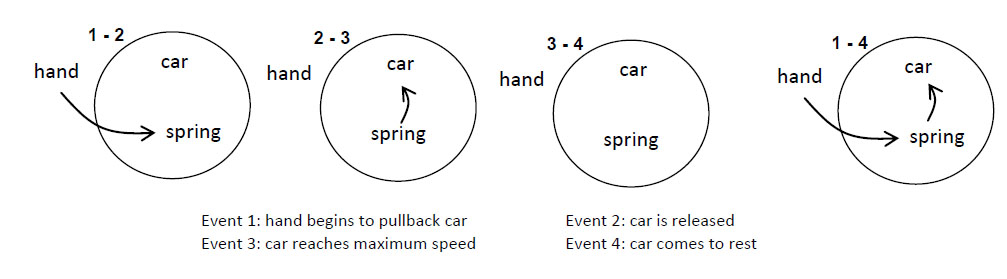
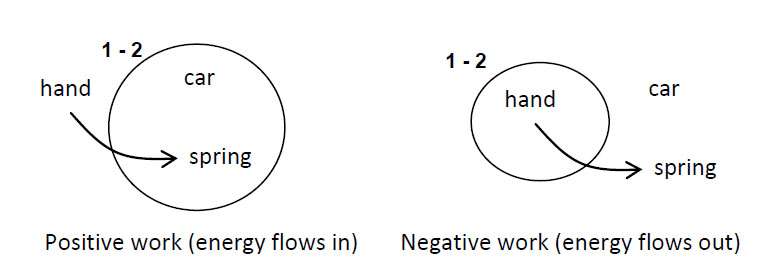
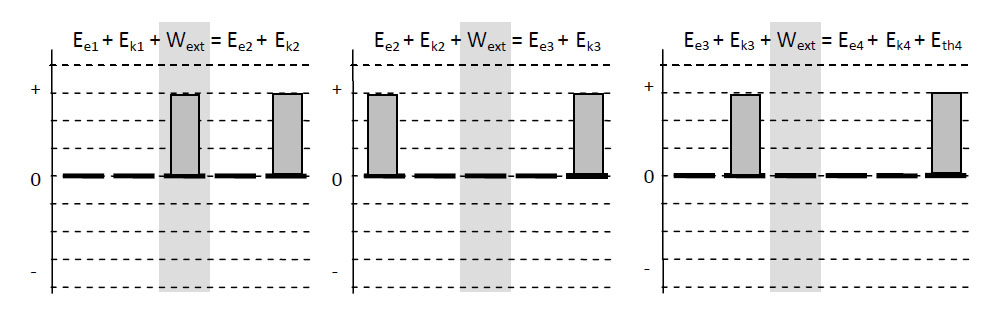Imagine a child, perhaps “Dennis the Menace,” who has blocks which are absolutely indestructible, and cannot be divided into pieces. Each is the same as the other. Let us suppose that he has 28 blocks. His mother puts him with his 28 blocks into a room at the beginning of the day. At the end of the day, being curious, she counts the blocks very carefully, and discovers a phenomenal law—no matter what he does with the blocks, there are always 28 remaining! This continues for a number of days, until one day there are only 27 blocks, but a little investigating shows that there is one under the rug—she must look everywhere to be sure that the number of blocks has not changed. One day, however, the number appears to change—there are only 26 blocks. Careful investigation indicates that the window was open, and upon looking outside, the other two blocks are found. Another day, careful count indicates that there are 30 blocks! This causes considerable consternation, until it is realized that Bruce came to visit, bringing his blocks with him, and he left a few at Dennis’ house. After she has disposed of the extra blocks, she closes the window, does not let Bruce in, and then everything is going along all right, until one time she counts and finds only 25 blocks. However, there is a box in the room, a toy box, and the mother goes to open the toy box, but the boy says “No, do not open my toy box,” and screams. Mother is not allowed to open the toy box. Being extremely curious, and somewhat ingenious, she invents a scheme! She knows that a block weighs three ounces, so she weighs the box at a time when she sees 28 blocks, and it weighs 16 ounces. The next time she wishes to check, she weighs the box again, subtracts sixteen ounces and divides by three. She discovers the following:

number of blocks seen + (weight of box − 16 ounces)/3 ounces = constant

There then appear to be some new deviations, but careful study indicates that the dirty water in the bathtub is changing its level. The child is throwing blocks into the water, and she cannot see them because it is so dirty, but she can find out how many blocks are in the water by adding another term to her formula. Since the original height of the water was 6 inches and each block raises the water a quarter of an inch, this new formula would be:

number of blocks seen + (weight of box − 16 ounces)/3 ounces + (height of water - 6 inches)/¼ inch = constant.

In the gradual increase in the complexity of her world, she finds a whole series of terms representing ways of calculating how many blocks are in places where she is not allowed to look. As a result, she finds a complex formula, a quantity which has to be computed, which always stays the same in her situation.²

Now let’s break down Feynman's story and explore a new conceptual framework for the teaching of energy.

Block party
One of the great struggles in the historical development of the idea of energy was the realization that all of the “different energies”, such as heat energy, kinetic energy, chemical energy, are really all members of the same family³, “energy“. Feynman described this with blocks in his story: the blocks are always just blocks and never change no matter how they are used. Mentally representing energy as blocks is the “quasi-material” part of this model and triggers within students valuable conceptual ideas associated with permanent, material objects. Intuitively, students will expect that blocks will not simply disappear and instead will just move around. This helps to make processes involving energy more concrete and easier to visualize. Blocks conceptually support the first law of thermodynamics, that energy cannot be created or destroyed. I regularly use the phrase “block of energy” in both grade 11 and 12 physics. I find it much more convenient than saying “one unit of energy” or “one Joule of energy”. After all, a joule is just a block of a particular size. The block idea helps to anchor the unified, indestructible nature of energy.

There is only one kind of energy and it is called “energy”
Yep. It's as simple as that. There is only one “type” or “form” of energy and it is called “energy”⁴. As Feynman illustrated, no matter where the blocks are stored or hidden, they remain as blocks: their nature has not changed in any way. The block model of energy provides a concrete way to understand the movement of energy. Energy moves, or flows, from one object to another and gets “stored” in different “mechanisms” Words like “kinetic”, “gravitational” and “elastic” are just labels for blocks of energy when they are stored in different mechanisms. I teach my students that saying “gravitational energy” is short form for saying “the energy stored in the earth's gravitational field”. Discussions about different forms of energy (how I used to begin the topic of energy) send a message that conflicts with the deep idea that there is just energy. This is not splitting hairs; it is laying a very careful conceptual foundation. All energy is stored in some mechanism, be it the motion of an object or its position in a gravitational field. The key idea is that there is just energy and it moves around, hiding in different places. Our job, as scientists, is to track it.

You can't beat the system
I used to begin teaching energy by writing something like: “Energy cannot be created or destroyed. The total energy of a closed system remains constant.” Students would ask me if that includes isolated systems and I would wonder to myself what the difference was and why they were asking. I never explained at all what a system was or how to use it, and never mentioned the word again. It was part of my formal definition for energy conservation, but somehow it was not a useful tool. The system concept is a foundational idea for physics: it is what allows us to make use of conservation ideas. Without clearly defined systems, conservation ideas are warm fuzzy feelings. We define a system as a collection of objects whose properties we want to keep track of. Once we have chosen a system, the real task of tracking energy can begin. Otherwise, you don't know where to look for energy, and don’t know whether to include it in your totals.

Looking for energy in all the right places
Unlike the blocks of Feynman’s story, we never get to see the actual blocks of energy. This is the main reason why we don't think of the energy blocks as real physical objects (an important point to highlight). Blocks of energy are a mental convenience. As scientists, we need to develop strategies to determine whether energy is stored somewhere and how much is stored. Dennis’s mother accomplishes this by looking for characteristics of an object or system that change when blocks are present. This is what scientists do and what our students must learn do: to associate the presence of energy with some observable property or change of state of the system. Otherwise, energy analysis becomes an act of faith rather than a practice of science. For example: suppose we observe the state of a ball changing and quantify this change by measuring its speed. This observation is our reason for believing that energy is now stored in the ball (in the motion of the ball). We label the energy stored this way “kinetic”. In this framework, energy is always stored in a particular location or object and there is always a measurable characteristic of the object which reveals its presence. All of these ideas are well supported by our block model and, very fortunately, physical reality.

Interaction energy
One important example of an energy storage mechanism is gravitational energy. When a ball travels upwards in the air and slows down, kinetic energy is decreasing (this is better to say than “losing” kinetic energy). So where is the energy going? There must be something that we can measure that reveals where the energy is. There is no change in the properties of any particles in the ball, so the energy is not stored there: it does not make sense to say ‘the gravitational energy of the ball”. Likewise, there are no changes in the particles of Earth, which leaves us scratching our heads. This is a challenging situation because the energy is somehow stored in the interaction between Earth and the ball. We can observe that the separation between the ball and Earth is changing, and this is related to the amount of energy stored in the gravitational interaction. When we do our later work, we write “Earth” as the location of the energy, with the understanding that this is a short form for “Earth’s gravitational field”. When speaking, I always say the full thing and make sure my students do as well. Also, I no longer use the word “potential” when describing energy, I just say “gravitational energy”: at this level of physics, the word “potential” does not provide any greater understanding.

Conservation of energy: glorified accounting
A great advance in the field of bean counting was double-entry bookkeeping. Turns out, keeping track of the individual ins and the outs is very helpful for understanding what is happening to the bottom line. Well, physicists are no more than glorified bean counters (OK, really glorified). Just stating that the total energy of a system does not change is fine, but it is really only true for the universe as a whole. It's the ins and the outs that really complete the picture of a system’s energy. In line with the first law of thermodynamics⁵ (and standard practice in chemistry), we state the conservation of energy as a change principle: choose two moments in time, the total energy at the second moment in time equals the total energy at the first moment plus any energy flow in our out of the system (the work done on the system by external forces). We call this the work-energy equation for the conservation of energy.

E_t1 + W_ext = E_t2

At this level of physics we don't worry about heating, radiation, and so on, but adding in another term would be a simple extension. This mathematical representation of energy has the form of a continuity equation, which is a very practical way to track energy and is pedagogically very desirable. It helps to connect mechanical work to the system energy, which was often a challenge for my students in the past. I remember them being able to perform separate calculations for work and system energy, but not having a clear idea whether the system was gaining or losing the energy (whether the energy was flowing in or out): they usually guessed. The work-energy equation with the block model helps students to visualize this: they can picture blocks of energy moving from object to object, or passing in or out of the system.

Picturing energy
This conceptual framework is quite deep and involved, especially compared with what I used to teach, but the sizeable pedagogical investment really pays off, especially after we introduce our picturing tools for energy⁶. The first specialized diagram students learn in grade 11 is an energy transfer diagram. It represents, in the most detail, the energy accounting of objects in the system and environment. The example below (the first example my grade 11s study) represents energy when a hand pulls back a spring-powered toy car, releases it, and the car rolls to rest. The blocks of energy are labeled with their particular storage mechanism at that moment in time and arrows show their movement. The dashed line represents the boundary of the system.

The diagram contains a lot of information, more than is typically needed when solving a problem, but provides the representational power to illustrate thorny situations like energy transfers due to sliding friction (coming up later, just wait!).

Go with the flow
We can simplify the energy transfer diagram to produce an energy flow diagram, one of our standard tools. In this representation, we hide the quantitative information and focus on the movement of energy. Here is a sequence of energy flow diagrams corresponding to the pullback car example.

Notice how they are coded for the successive moments in time — a flow diagram can be created for any pair of moments. Being clear and precise about the selection of moments is critical for an accurate accounting of energy and its representation. This is not a trivial issue — just like knowing whether to close your fiscal books on December 31^st or March 31^st, it makes a difference, especially when the government takes an interest in what you have been earning. We build up the skill of choosing events with precise moments of time from the start of grade 11 physics and practice this skill a lot. Once events are carefully chosen, energy flow diagrams make clear whether the system is gaining or losing energy. This understanding becomes very important for making sense of the mathematics later on.

Time to hit the bar
A different way of simplifying the energy transfer diagram is creating a work-energy bar chart. This approach focuses on the quantitative analysis of energy and provides a powerful tool to help students construct correct equations for problem solving. Below are bar charts from the pullback car example.

One side of the bar chart represents the energy stored in system objects at the first moment in time, the middle bar represents the work done on system objects by external forces, and the second side represents the energy stored at moment two. Students construct bars for the relevant storage mechanisms and use these to decide how to construct a work-energy equation. This has been a great support for my students’ mathematical work. In the past they would haphazardly include mathematical terms in their work-energy equations or just memorize one instance of it and apply it to every situation (sound familiar?). The icing on the energy picture cake is that bar charts and flow diagrams allow students to cross-check their understanding of the energy processes that are present.

All warmed up for thermal energy
Nothing warms the cockles of my heart like thermal energy, a most mischievous form of energy. Consider our car example again: we observe the car slowing down, and the kinetic energy decreasing. Our hope is that the energy stored in the motion of the car has not just disappeared. There must be a change in the state of something that we can measure to track down the energy. Careful inspection with an infrared thermometer pointed at the internal mechanisms of the car would reveal an increase in temperature. Very careful scientific work, done about 180 years ago⁷, now convinces us that the energy once stored in the bulk movement of the car is now stored in the random vibrations of the atoms of the car. This is our physical model for this stealthy storage mechanism for energy. It is important for students to go through this thinking process, even though any changes in the temperature of the car are likely too small to measure⁸.

Energy lost
One facet of energy that the block model does not accommodate is any description of the quality of the energy, or how useful it is for doing mechanical work (all models have shortcomings). In the car example, the quality of the energy degrades; it becomes more disorganized, yielding an increase in entropy⁹. This energy is still in our system at the final moment we have chosen and should not be described as “lost”, which would be the equivalent of cooking the books. The energy is certainly much less useful, but lost it is not. It is beyond the scope of high school physics to detail what happens to the thermal energy after our final moment, although a brief discussion of this is valuable. The energy is not lost, but transfers to the environment through a variety of mechanisms. A new label can be applied to energy that remains highly organized while it transfers back and forth: mechanical energy. As long as the system total of mechanical energy does not change, the system will have the remarkable property of path independence. Never say “mechanical energy is conserved”: I know what you mean, but students don't. We must make a serious effort to eliminate such loose language. Mechanical energy is not a conserved quantity, mechanical energy can be destroyed. Only a few special things in this universe are conserved, so let’s keep that club exclusive. Along the same lines, when discussing elastic collisions, rather than saying “kinetic energy is conserved” (which it really, really isn't), say “the system total of kinetic energy before and after the collision is the same” — wordy, but actually correct.

Students and their thermal energy
Student’s work with thermal energy needs to be treated with great care, and some measure of forgiveness at our level of study. In the energy flow diagrams shown above, the keen-eyed reader might have noticed that the transfer to thermal energy seems to occur exclusively during the slowing of the car. This is not correct, but in my books qualifies as close enough. A cleverer student might show small transfers to thermal energy at each step along the way. While more correct, they will struggle when it comes time to work mathematically with their complex representation. With my students, I acknowledge this continuous transfer to thermal energy (and other forms like vibrations and sound), and then ask them to keep it simple as I have shown in my energy flow diagrams. This is justified because at the end of this series of processes, the vast majority of energy stored in the spring is now stored as thermal energy. In grade 12, I introduce a catch-all label “internal energy” in the context of inelastic collisions to cover all the many forms of energy that the kinetic energy transfers to.

Time for work
Now for the grand finale. Work is a deceptively simple idea with a wealth of nuance and subtlety. My students first encounter work as the label for the energy flow from one object to another due to a pair of forces (an interaction). Through this interaction one object gains energy and the other loses (the system total of one increases and the other decreases — double entry bookkeeping!). To understand which side of the flow we are talking about, we must choose a system. There is so much confusing language about work done “by the force” or “on the object“. Make clear the choice of system and always describe the work as work done on a system object by an external force: the confusion will be gone. With the pullback car example, if we choose the car as the system, the system gains energy while the hand exerts a force on it and drags it backwards (positive work). If the hand was the system, it loses energy and experiences negative work. Notice the arrows are the same.

We later connect this to the mathematical definition of work, noting the angle between the force of the hand and displacement of the car. We approach the topic of energy just like all the other topics in physics: we introduce the concepts first and then construct the mathematical framework around it.

Working the system
The composition of the system determines how we interpret the results of work. If the system can be modelled as a point particle, the total work equals the change in the particle’s kinetic energy. This is known as the net work-kinetic energy principle, which is a special case of the more general work-energy equation and is valid only for point particles (or the system centre of mass). However, we often choose systems with a collection of objects where the work cannot be interpreted in terms of the change of kinetic energy. For example, consider lifting a book vertically. Without realizing it, most of us usually choose a system consisting of the book and Earth’s gravitational field. The evidence for this is the typical work-energy equation that represents this situation:

½mv₁² + mgy₁ + W_ext = ½mv₂² + mgy₂

This statement reveals that we are tracking the energy stored in the book and Earth's gravitational field, as shown more carefully in the diagrams below.

These are the objects of the unspoken system. Regardless how clear the traditional approach is in our own heads, it is confusing for our students when we do not clearly state the system and take it seriously! (In my own experience, I now understand that the traditional approach was not clear, even to myself: I had never bothered making sense of the energies because I was getting mathematically correct answers. Mathematics can be a great impediment to understanding if the right conceptual tools are never taught.) I can remember when I taught the old way, my students always asking which side of the equation the term for work should go on. Without a clear sense of the system that underlies the equation, they were usually just guessing. Returning to the book example, suppose the book is moving at a constant velocity. In this case there is work done on the system, but the kinetic energy is not changing. This is an example where the net work-kinetic energy theorem is not valid since the system is not a single point particle. In my current teaching practice, I rarely use the net work-kinetic energy theorem — it is just a special case of the work-energy equation and does not deserve much emphasis.

As an interesting comparison, we can choose the book alone to be the system.

In this case there are two external forces doing work on the book, the applied force of the hand and the force of gravity of Earth. One force does positive work, the other negative work, yielding a total work of zero. The kinetic energy of the book does not change showing that the net work-kinetic energy theorem is valid. Notice the arrows in the two flow diagrams are the same as the previous for diagram with the original system (all the flows are the same). But note that the only system energy being tracked is that of the book. The gravitational interaction must be shown as negative work, rather than an interaction energy of the system.

Displacement? What displacement?
Let's return one last time to the pullback car and consider the interval of time when the car is slowing down. From a force perspective we explain that the car slows down due to an external force of friction (rolling friction) between the wheels and the table. This leads us to the temptation of saying that the force of friction is doing negative work on the car, causing it to slow down. Based on our understanding of mechanical work, this implies a flow of energy from the car to the table. But try as we might, we cannot find any change in the properties of the table: there was no change in the table’s energy. There is, however, a change in the properties of the car: the warming of its internal mechanisms. Consider the brakes of a real life car: try touching the rotors in the brakes after you have driven a while. (Note: touching the rotors of your brakes after you have driven a while is not a good idea, however educational it might be: do so at your own risk. I've done it.) The flow of energy did not seem to behave according to our understanding of work. An external force was acting on the system, but the energy remained in the system. This is also the case for walking along the floor: the interaction between the floor and your foot exerts a forward force on your foot and you speed up, but there is no transfer of energy from the floor to you. In these two examples, the systems have internal degrees of freedom (moving parts, internal energy storage mechanisms). We must refine our understanding of work by examining the displacement more carefully. Consider a particle of the foot that is in contact with the floor. While the friction force from the floor is acting on that particle, the particle has no displacement along the floor. No displacement means no work or energy flow. With complicated systems, we must use the displacements of the particles the external forces act upon, not the system centre of mass.

Work and sliding friction
Another cautionary tale involves sliding friction. Suppose the brakes of your car locked and the tires skid across the road surface. A traditional analysis focusing on mechanical energy with the car as the system gives an equation:

½mv₁² + W_f = 0, or W_f = –½mv₁²

Our understanding of forces tells us that the friction force between the car and the road surface causes the car to stop. The “energy equation” above suggests that the amount of work done is equal to the original amount of kinetic energy, but this is not correct. This equation is derived from Newton’s second law and is based on force ideas rather than energy ideas. To properly describe the flow of energy out of this system we must fully account for all the energy in the system (which Newton’s laws cannot do) by constructing a proper work-energy equation based on the conservation of energy.

½mv₁² + W_f = E_th, or W_f = –½mv₁² + E_th

The result looks similar, but we introduce an important term for the thermal energy that is present in the car the moment it stops. This equation tells us something very surprising: that the amount of work done by friction is less than the amount of kinetic energy (E_th is positive). A direct calculation of the work done by friction using the equation for work in the traditional way will not give its correct value. Due to microscopic deformations of the tire and road surfaces while sliding, the displacement of the surface particles in contact is always less than the displacement of the object. So the friction interaction between the surface and the tire causes less energy to flow out of the system (less work) than we expect because some energy remains in the system as thermal energy. For example, if the car had 50 000 J of kinetic energy, perhaps 20 000 J flowed out, with 30 000 J remaining in the system as thermal energy stored in the hot tire surface. The 20 000 J that left the system is stored as thermal energy in the road surface (assuming no energy used to break up the tire surface, create sound, etc.). For more on this, I encourage you to explore the textbook Matter and Interactions¹⁰ and the author’s research papers^11,12.

The amount of work done by a friction force cannot be easily found from the definition of work unless you know true microscopic details of the surface particles in contact. As a result, there is no simple way to predict how much energy actually flows out of the system due to the friction force. In situations such as these, I instruct my students to include the surface as part of the system so in our accounting of energy, all the energy remains in the system (E_k1 = E_th) and we don’t have to worry about partitioning the thermal energy between the two sliding surfaces.

Even though we can't find the work done by friction, we can find the transfer to thermal energy due to the friction force: E_th = F_fd, where d is the distance traveled. This result is based on a careful analysis that takes in to account the smaller displacement of the surface particles during sliding friction^13,14. Notice that it has the same numerical result as the traditional work calculation, but provides a correct physical understanding of the energy processes taking place. This is another example where our traditional approach has given us correct results mathematically (we can find the distance it would slide given a certain friction force and kinetic energy), but has not helped us understand what is happening physically. And who are we anyway, math teachers or physics teachers?

The energy in the room
I spent years wondering why my students had such difficulty with simple problems involving energy. Now I understand that the problem was actually with my presentation of the topic: a lack of clear conceptual framework, ideas that weren't tied together, and my own weak understanding. Energy is conceptually very challenging: Newton failed to produce a framework for energy and the efforts of dozens more were required to piece together our modern understanding of it. Physics education research made is earliest advances focusing on forces and motion and is only now generating the pedagogical insight we need to reform our teaching of energy. Personally, I have found energy to be the most difficult topic to teach using an internally consistent framework and the writing of this article has helped me put to rest my final doubts and concerns. All of this pedagogical effort only has value if it leads to improved understanding with my students. This is very difficult to gauge in a quantitative way, but my observations of student discussions and written work leave me encouraged. Students pick up the picturing techniques quite quickly and these really help them with the math work. During lunch I have seen discussions breakout amongst students where they use the diagrams spontaneously.

It is challenging to teach in a conceptually new way and has taken me many years to fit all these pieces together. You can take the shortcut: take a look at my grade 11 and 12 lessons in our physics handbooks and check out the videos of these lessons in action. All of this can be found on my website: www.meyercreations.com/physics. The door of my classroom of always open and you are most welcome to drop by and talk to my students about energy, just send me an email and we can set up a day.

References
1 Scherr, Rachel E., et al. "Representing energy. I. Representing a substance ontology for energy." Physical Review Special Topics-Physics Education Research 8.2 (2012): 020114.

2 Feynman, Richard P., Robert B. Leighton, and Matthew Sands. The Feynman Lectures on Physics, Desktop Edition Volume I. Vol. 1. Basic Books, 2013.

3 https://en.wikipedia.org/wiki/Conservation_of_energy#History

4 Swackhamer, Gregg. "Cognitive resources for understanding energy." (2005).

5 https://en.wikipedia.org/wiki/Conservation_of_energy#First_law_of_thermodynamics

6 Scherr, Rachel E., et al. "Representing energy. II. Energy tracking representations." Physical Review Special Topics-Physics Education Research 8.2 (2012): 020115.

7 https://en.wikipedia.org/wiki/Conservation_of_energy#History

8 Daane, Abigail R., et al. "Energy conservation in dissipative processes: Teacher expectations and strategies associated with imperceptible thermal energy." Physical Review Special Topics-Physics Education Research 11.1 (2015): 010109.

9 Daane, Abigail R., Stamatis Vokos, and Rachel E. Scherr. "Goals for teacher learning about energy degradation and usefulness." Physical Review Special Topics-Physics Education Research 10.2 (2014): 020111.

10 Chabay, Ruth W., and Bruce A. Sherwood. Matter and interactions. John Wiley & Sons, 2015.

11 Sherwood, Bruce Arne. "Pseudowork and real work." American Journal of Physics 51.7 (1983): 597-602.

12Sherwood, Bruce Arne, and W. H. Bernard. "Work and heat transfer in the presence of sliding friction." American Journal of Physics 52.11 (1984): 1001-1007.

13 Serway, Raymond, and John Jewett. Physics for scientists and engineers with modern physics. Cengage learning, 2013.

14 Jewett Jr, John W. "Energy and the confused student I: Work." The Physics Teacher 46.1 (2008): 38-43.

Tags: Energy, Pedagogy