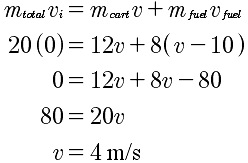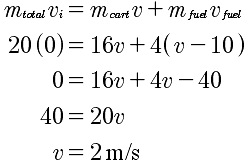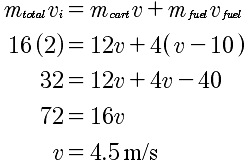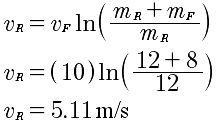John Berrigan, Teacher Oakville Trafalger H.S.
berriganj@hdsb.ca

Interest in rockets is skyrocketing due to the recent successes of SpaceX and Blue Origin, two private companies developing spaceflight. This is an ideal time to introduce students to the physics behind rockets which are an exciting illustration of the conservation of momentum and relative motion.  

To motivate your students and yourself, take a look at where private technology — not NASA — is today. These two videos are from April 2016.

SpaceEx


Blue Origin


A rocket is similar to the recoil of a gun from a bullet being fired, except that in a rocket engine the fuel is not all thrown out at once, but in a continuous flow.  Let’s start with a simple example. Suppose we have a 12 kg cart on a frictionless surface that has the ability to throw an 8 kg mass off itself at 10 m/s relative to the cart. Those last three words are critical! We don’t know the velocity of the cart after the throw, so we will give it a velocity “v” relative to the ground. That means the 8 kg mass will have a velocity of v – 10 relative to the ground.

Drawing a diagram really helps in solves these types of problems.



The momentum before must equal the momentum after, so


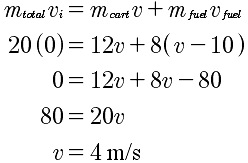
What happens if the mass is thrown off in two 4 kg chunks?



After the first throw;




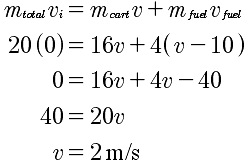
After the second throw


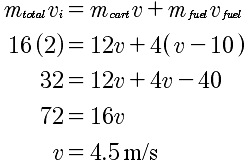
Notice that the final velocity is faster! We can repeat this procedure for smaller and smaller chunks and the final velocity should get larger and larger. Is there a limit to this speed? I have made a simple simulation that will allow your students to explore this and other questions more easily. 

Cart velocity = 0 m/s; Fuel Velocity = 0 m/s
Throw	Reset
Cart mass = 12 kg	Fuel mass = 8 kg
Number of throws = 2	Vel. of throw = 10 m/s

cart mass,cart velocity,fuel Velocity

Hit the ‘throw’ button and then hit it again. The results after each toss are shown below the animation. Throwing the eight kilograms in one throw gave the cart a speed of 4 m/s and two throws gave it a speed of 2 and then 4.5 m/s. What speed will you get with three throws? Try it. What about four throws? The students will notice when there are more throws, the increase after each throw is less but since there are more throws the final velocity is always faster.

What is the fastest possible final velocity that can be achieved? The smallest mass that can be thrown off is an atom. (This type of engine is called an Ion Engine) Calculating the speed atom by atom would be tedious even with the simulation. Fortunately, calculus allows us to develop a formula for the final increase in speed of the rocket AKA the rocket equation;



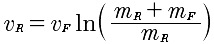
Where, v_R = velocity of the rocket relative to the ground, v_F = velocity of the fuel relative to the rocket, m_F = mass of the fuel ejected and m_R = final mass of rocket and any fuel remaining on board.

What is the largest possible value for our example?


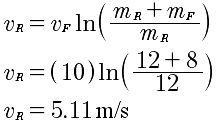
Next up in this series I will explain the factors involved in rocket thrust.  Eventually, if you let me, I hope to show you how we can get to Mars!!  Ad Astra!!

Tags: Momentum, Motion