Dave Doucette, OAPT Vice-President
doucettefamily@sympatico.ca

While teaching uniform circular motion in high school, I struggled with developing the a_c = v²/r relationship in an intuitive and cognitively meaningful way. Geometric arguments do not resonate with students. They accept on faith but often with little interest or insight. Here is an approach that may do a better job.

If we approach it from the perspective of contextual learning¹, using simple vector analysis, the relationship can have a more constructive context. To maximize student discourse, have students sketch out the following diagrams on their group whiteboards. In this exercise, in addition to the explicit practice of subtracting vectors and dividing by scalars, students use vector analysis to construct meaning, a level of reasoning which can help anchor concept attainment².

Begin with a pictorial sketch of the circular path of an object traveling at constant speed. Place a velocity vector, V₁, at one instant and V₂ a quarter of a period later. This should something like the pictorial representation shown below on the left.



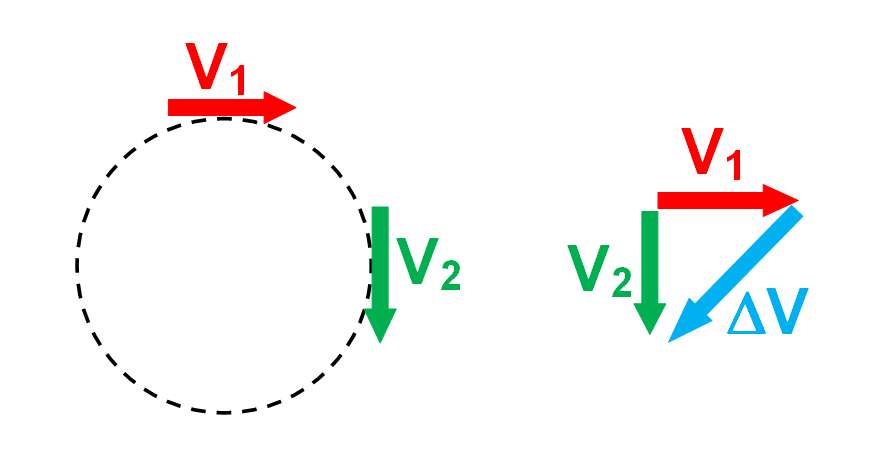
Acceleration is the change in velocity/change in time, or ΔV/Δt. Have the students translate the pictorial vectors to a mathematical vector diagram and apply the rules of tail-to-tail vector subtraction to find ΔV. This is shown above, on the right.

Finally, have the students divide ΔV by the scalar time, Δt, which is required for the object to move from position 1 to position 2. The division of a vector by a scalar remains a vector quantity, with the same direction but different units and a different quantity. This should be explicitly reinforced. Vector analysis is often introduced with very little context, resulting in students memorizing procedures but not appreciating the connection to physics concepts. When teaching is deliberate — in high value areas such as unpacking the relationship of mathematical algorithms to concepts — student learning moves forward.

Proportionality of v to a_c
The next step is to double the velocity, but maintain the same path radius. The diagram changes in that V₁ and V₂ double as does ΔV, as seen below:


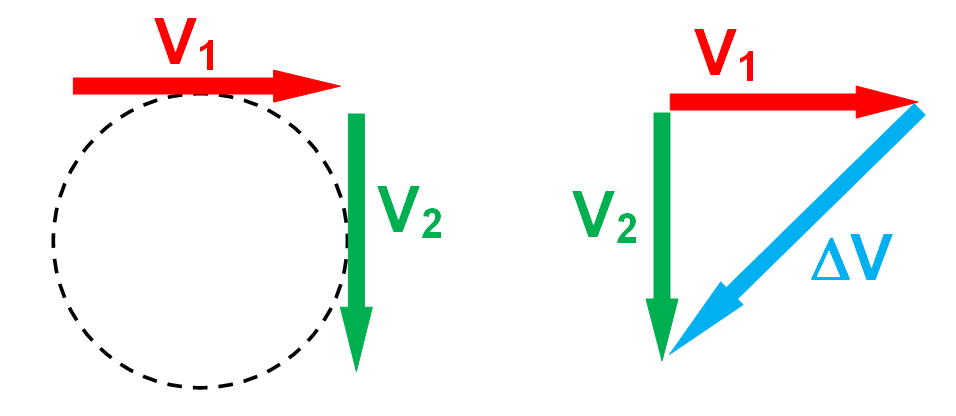
A doubling of the velocities produces a doubling of ΔV. When I ask the students to predict the effect on the acceleration, most conclude the acceleration must have doubled. In explanation, one student stated, “Since the delta V is twice the initial value, the acceleration must also be double.” When asked if the direction of ΔV has changed, they inspect the diagrams and recognize that the 45° angles are due to equal vector lengths and conclude that direction is unchanged. I inform them they are entirely correct in their reasoning but incorrect in their conclusions and then challenge them to determine why.

Soon after, a group will notice that the time to travel from position 1 to position 2 must have changed. “If they travel the same distance at twice the speed, they must arrive in half the time. So the time must be ½ the first time, Δt/2.”

“What will this do to the acceleration?” I ask. “Double it,” they reply, after a brief moment to ponder.

“So if the change in velocity is doubled AND the change in time is reduced to one-half, what is the effect on acceleration?” They quickly recognize the acceleration must have increased four times.

I then assign various groups to change the velocity by 3, 4, 1/3, etc. until all groups are assigned a unique value for the initial velocity. They repeat the process to determine the effect on acceleration. They record their results and we examine the class pattern. Tripling the velocity results in 9 × a_c, quadrupling results in 16 × a_c, and 1/3 v produces 1/9 a_c .The proportionality of a_c to v² is revealed. Ultimately students are led to conclude that centripetal acceleration is proportional to the square of the velocity.

Proportionality of r to a_c
The second factor to consider is radial length, r. Changing the radius of the circle but maintaining the same vector lengths for velocity will produce identical ΔVs. But the time to travel ¼ of the path around a circle of twice the circumference will take twice as long, 2∆t.



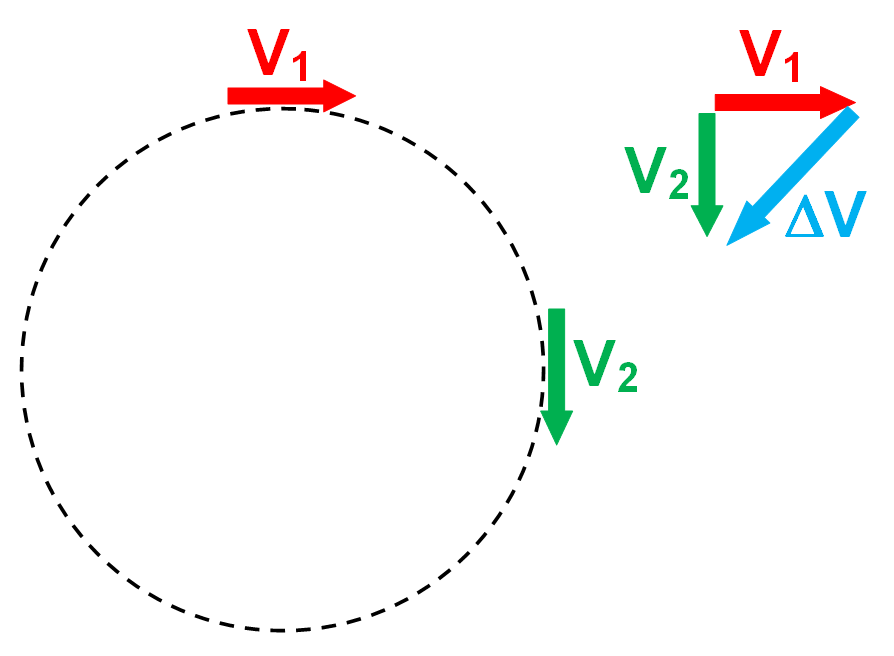
Dividing ΔV by 2∆t will result in a value of acceleration of ½ a_c. The effect of 3r, 4r, ½r and so forth on a_c can also be quickly ascertained. Acceleration will be seen to change in inverse proportion to the change in time, i.e., a_c is proportional to 1/∆t. Combining the changes in V and r justifies the expression:

a_c = v²/r

The intellectual effort and the essential student discourse provides time and opportunity for the brain to properly integrate this deceptively challenging act of analytical reasoning.

Modes of Reasoning
I pointedly differentiate between a “pictorial vector diagram” and a “mathematical vector diagram”, two separate but related modes³ of perception. In physics we incorporate diagrams upon which we superpose numerous vectors. Students need to learn how to correctly label and place vectors to give meaningful context to a diagram. At the same time students are learning the rules of mathematical operations on vectors. To shift analysis to a “mathematical vector diagram”, vectors are copied from the pictorial diagram, deliberately redrawn and ‘operated on’ by the rules of addition, subtraction and multiplication of dot and cross products. Encouraging students to attach vectors to a pictorial diagram and separately sketching related mathematical operations helps them transition between these two modes of reasoning, fostering the growth mindset from novice toward expert problem-solvers⁴.

The last important concept is how the direction of the acceleration is related to the velocity. In the specific example shown, the acceleration was at 45o to each of the velocities. Ask the students, what the angle would be if the velocities were apart by 30°, 10° or 1°. Finally, what would it be for 0°? Rather than a detailed treatment of limits at this stage, simply advise them that calculus will explore and expand the concept of limits. Tread softly to avoid muddying the understanding achieved by the a_c exercise.

No doubt this method has been applied by teachers before but was a new discovery for me and may be helpful to others.


References

1. Johnson, E; Contextual Teaching and Learning; Corwin Press, 2002.
2. Johnson, J; Carlson, S; Kastl, J; Kastl, R; “Developing Conceptual Thinking: The Concept Attainment Model”; The Clearing House: A Journal of Educational Strategies, Issues and Ideas, Vol 66, Issue 2, 1992.
3. McDermott, M; Hand, B; “The Impact of Embedding Multiple Modes of Representation Within Writing Tasks on High School Student’s Chemistry Understanding”, Instructional Science, Vol 41, Issue 1, p 217-246, 2013.
4. Larkin, J; McDermott, J; Simon, D; Simon, H; “Expert and Novice Performance in Solving Physics Problems”, Science, Vol 208, p 1335-1342, 1980.
   

Tags: Kinematics, Motion, Pedagogy