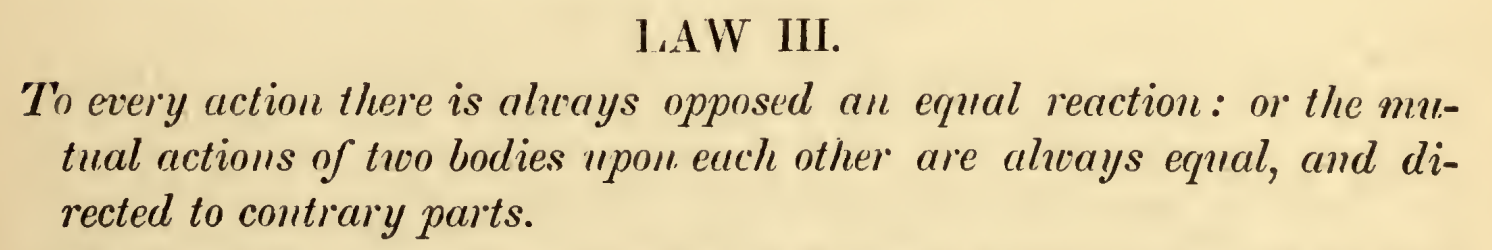Roberta Tevlin, OAPT Newsletter Editor, Teacher at Danforth CTI
roberta@tevlin.ca

One of the standard parts of an introductory physics course is a study of Newton’s Three Laws of Motion. They are part of the Ontario curriculum for grade 11 physics and most teachers would agree that they are essential. Chris Meyer has presented an improved way to teach the three laws of motion that will deepen student understanding: Teaching Forces I and Teaching Forces II.

In this article, I hope to reinforce Chris’ approach with a look at how the history of these three laws is wrongly presented.

Let’s start with what Newton (1687) actually wrote in the Philosophiæ Naturalis Principia Mathematica, commonly known as the Principia. I don’t read Latin, so I used the final edition as translated by Andrew Motte. I have made screen shots of the critical entries, but the full thing can be found here. (Note: This source starts with a Life of Newton. The Principia doesn’t start until page 77.)

What Did Newton Write? Part 1:


We commonly refer to the first law as the “law of inertia”. Discussions about inertia had been around for decades before the Principia was first published in 1687. For example, Isaac Beeckman wrote about it in his journal sixty-nine years earlier. However, he didn’t publish his thoughts because of a nasty campaign by Rene Descartes accusing him of plagiarism (Arthur, 2002). Descartes wrote about the principle in The World where he improved Beeckman’s concept of inertia by showing that a circular motion needs a central force. This work was also not published, in this case because Descartes was afraid of the church’s response to his Copernican views of celestial motion. His thoughts finally appeared in the Principles of Philosophy (see https://plato.stanford.edu/entries/descartes-physics/). This book, published forty-three years before the Principia, describes three laws of nature. The first two were essentially Newton’s first law broken into two parts and the third was very similar to Newton’s third law of motion.

The first discussion of inertia that appeared in print was Galileo’s Discourses and Mathematical Demonstrations Relating to Two New Sciences in 1638. Some of Galileo’s thought experiments were tested experimentally by Pierre Gassendi who fired and dropped metal spheres while on a ship moving at a constant velocity. These results were published in his De motu impresso a motore translato of 1641. For further discussion, see this entry in the Stanford Encyclopedia of Philosophy.

It is clear that Newton’s First Law of Motion was not his. Perhaps we should call it the Law of Inertia. However, Chris Meyer makes a good argument for dropping the term “inertia” altogether. This term confuses students (as it did many scientists in the past) and they think of inertia as another kind of force.

What Did Newton Write? Part 2:


That doesn’t look anything like F = ma! We need to do a little unpacking here. Newton explained what he meant by ‘alteration of motion’ in one of the definitions that precede the three laws.



According to Newton, the ‘quantity of motion’ includes the velocity and the quantity of matter, or what we would call mass. If we assume that it is proportional to each then this is the momentum. Therefore, his second law states that the change in momentum, Δ(mv), is proportional to F. This still not F = ma because it is missing is the time interval.

Newton did not use calculus or algebraic expressions in the Principia. Instead, he used geometric arguments. He couldn’t show time in his diagrams, so he showed the difference in position that resulted from a force. Time was implied in his arguments but never made explicit.

This was perhaps a step backwards. Forty-nine years earlier, Galileo provided quite a lot of algebraic analysis in his Discourses and Mathematical Demonstrations Relating to Two New Sciences. He showed that a falling object experiences a constant acceleration and will have a speed proportional to the square root of the height of the drop. He tested this analysis using spheres rolling down an inclined plane and it became known as Galileo’s Law of Falling Bodies. He also combined this accelerated motion with the constant horizontal motion of a projectile and showed that its path would form a parabola.

It was Jacob Hermann who first showed that F = Δ(mv)/Δt in his Phoronomia of 1716 (Smith, 2007). If mass is constant, then Δ(mv)/Δt = mΔ(v)/Δt = ma and therefore F = ma. However, Newton never wrote F = ma, not even in his third edition, which appeared ten years after Hermann’s result was published.

Perhaps we should just call Newton’s Second Law, the law of acceleration or as Chris Meyer recommends, the law of cause and effect.

What Did Newton Write? Part 3:


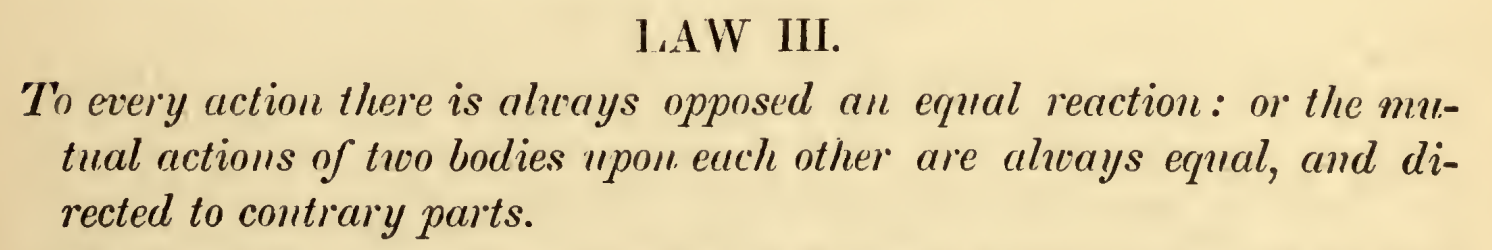
Most textbooks quote the first part of this law and not the second. However, the terms ‘action’ and ‘reaction’ are problematic because they suggest some conscious effort with the action and delay in the reaction. The second part is much better because it emphasizes the symmetry when two bodies interact.

Newton explains what he means by the word ‘action’ in his fourth definition.



If an ‘action’ is a ‘force’, then Newton’s third law can be written as “When two bodies interact, the force is exerted on each of them in opposite directions”.

Newton provides a very nice example of the symmetry in an interaction.



The rope makes the force-pair more obvious. A great way to do this in class is to use an elastic band which also shows a visible extension that increases with an increased force.

However, when Newton wrote ‘action’ he meant more than just the ‘force’ as this next part shows.



As we have already learnt, the term ‘motion’ means momentum. Therefore, he is talking about the change in momentum, Δp, and this means that the ‘action’ must mean what we now call the impulse, FΔt. His third law is not just about force pairs, it is an expression of the exchange of momentum and leads to the concept of the conservation of momentum.

Descartes was the first person to write about a conserved quantity of motion. His third law of nature in the Principles of Philosophy (1644) describes that there is a conserved quantity of motion which involves the size and speed of each body in the interaction. Newton’s third law improved Descartes’ third law by replacing size (volume and area) by the mass of the body and replacing speed with velocity (Slowik, 2017).

Newton’s Third Law of Motion owes a large debt to Descartes and it should be broken down into two parts. The first part refers to forces and is found in the grade 11 curriculum. The second part involves FΔt = Δ(mv) and is covered in the grade 12 curriculum. Newton did not consider FΔd = Δ(E), which is taught in grade 11. This idea took almost another century to be clarified and accepted.

What Did Newton Write? Part 4:
The Principia starts out with eight definitions, four scholia (comments), three laws of motion and six corollaries. Following all this, there is another scholium which contains this selection.



Newton is stating that what he has been writing about is nothing new! Further down you find this.



Once again, Newton is making sure that the reader realizes that he is not claiming this work as his own. This is ignored in most textbooks. Some mention Galileo, but otherwise they give Newton all the credit.

I am surprised that Newton does not mention Descartes, given how similar their three laws are. Perhaps it was because Descartes had already died and wasn’t as well known in science as Galileo was.

How should we teach the Laws of Motion in high school?
First, do not call them Newton’s Laws of Motion. Even Newton says that they are not his. Secondly, do not use his old-fashioned language if there is a clearer way to say it. Finally, do not number them or teach them in the order that he used if there is a better way to scaffold the learning. Here is a suggestion;

1st Law: An object will continue moving at constant velocity unless a force acts on it.
This is just a statement that the default behaviour of matter is to continue doing whatever it was doing. It includes not moving. If it is moving, the direction as well as speed stays the same.

2nd Law: Interactions between two objects involve a force exerted in opposite directions on each object.
There is one force in the interaction but it gives rise to an equal and opposite force pair when you consider how it acts on each object. This law is the first part of Newton’s Third Law. It is in second place because an exploration of what forces are should come before the use of forces in F = ma.

3rd Law: F_net = ma.
This is usually called Newton’s Second Law. It has had time explicitly added to it.

Details of this approach can be found in Chris’ two articles Teaching Forces I and Teaching Forces II.

4th Law: During an interaction, FΔd equals the change in energy.
This understanding of energy was not fully developed for a century after the Principia was first published. When the energy changes are closely measured, it leads to the idea that energy is conserved. It has been placed fourth and not fifth because in Ontario it is taught in grade 11.

5th Law: During an interaction, FΔt equals the change in momentum.
This is the second part of Newton’s Third Law and it is found in Ontario’s grade 12 curriculum. When the change in momentum is examined, it leads to the idea that momentum is conserved. When it is taught, students should review the fourth law and compare the two. Students should also review F = ma and see that it is a special case of FΔt = Δ(mv).

What should students learn about the history of physics?
They shouldn’t learn that Newton single-handedly came up with calculus, the three laws of motion, circular motion, universal gravity, the refraction of light and the ‘discovery’ of indigo in the rainbow. They should hear about some of the other people who were deeply involved in developing our understanding.

One great example is Emily du Chatelet. In 1749 she completed a translation of the Principia from Latin into French, which played a critical role in spreading his ideas. As well as translating the language she also translated his geometry into other forms including simple equations and calculus. She added lots of detailed commentary that made his work much easier to understand and she extended his work to include energy. She worked up to 20 hours a day in order to complete this work before dying in childbirth (Zinsser, 2006).

The stereotype of the solitary genius doing it all is simplistic and false. It is contrary to the way science is done and it suggests that only the very brightest people should consider doing physics. This misleading stereotype is very damaging and can turn students off before they have given physics a proper try.

I would like to end by thanking Chris Meyer and Phillip Freedman who engaged in some lengthy email discussions during the summer that helped me greatly in my research, understanding and writing. All errors and excesses are my responsibility.


References
Arthur, R. (2002). “Beeckman, Descartes, and the force of motion”. Retrieved from https://www.humanities.mcmaster.ca/~rarthur/papers/BDFM.pdf.

Newton, I. (1687). Philosophiæ Naturalis Principia Mathematica. Translated by Andrew Motte. Retrieved from https://ia802706.us.archive.org/0/items/newtonspmathema00newtrich/newtonspmathema00newtrich.pdf

Slowik, E. (2017, August 22). “Descartes' Physics”. Retrieved from https://plato.stanford.edu/entries/descartes-physics/.

Smith, G. (2007, December 20). “Newton's Philosophiae Naturalis Principia Mathematica”. Retrieved from https://plato.stanford.edu/entries/newton-principia/#NewLawMot.

Zinsser, J. P. (2006). La dame d’Esprit: A biography of the Marquise Du Chatelet. Viking: New York.

Tags: Forces, History, Kinematics, Motion, Pedagogy, Projectile Motion