Chris Meyer, President, Ontario Association of Physics Teachers
Christopher.meyer@tdsb.on.ca

Here is a rich problem solving activity that I use when introducing the five equations of constant acceleration with my grade 11s.

Goal: I want to teach my students how to apply their new understanding to real physical situations and avoid plug’n’chug type questions.

Setup: We have an inclined track set up at the front of our class with a motion detector at the top. I release a cart from rest at the top and determine its acceleration from a velocity graph. The acceleration is the only information I give the students.



Challenge: The students’ challenge is: choose a position along the track and predict the velocity of the cart at that position. Simple, eh? You can see the sticky-notes marking students’ chosen positions in the image above.

Design Rationale: It’s not simple! Since I only give my students one piece of information (the acceleration), they cannot quickly plug’n’chug an answer. Instead, they must physically reason about the situation, examine the set-up, and decide on what information to use. This more closely models real-world problems and the thinking of experts. Also, each group of students has a different final position, so they can’t just copy answers from one another and short circuit their learning.



Students construct a solution to the problem using our standard solution process that they are now very familiar with. This process prompts them to carefully explain their understanding and make connections between different representations of motion (e.g. sketch, motion diagram, position graph, velocity vectors, math). The process also encourages them to present their mathematical work in a thoughtful way that explains their reasoning. This is a complex process with which students need lots of feedback. Once they have a prediction (a complete solution), students compare their work with a model solution and add corrections or improvements (descriptive feedback) to their work using blue pens (they work in pencil); their original work must still be visible.

What do students have to say about "using the blue pens"? I put this question on our motion unit test:





Notice that no numbers are in the model solution! Next, students record their group’s prediction on the sticky-note attached at their chosen position. They still don’t know if they are “correct”.



Take a look at the image above (using the powers of science I fudged one of the sticky-notes to show what often happens, but didn’t happen this time around!) Students don’t know the “correct answer” yet, but there is some very helpful information available. Without me hinting, they begin to notice how their prediction fits into the overall pattern. Students usually notice when their prediction falls outside of the pattern (the simulated image above) and return to their work to look for problems. The more often students check and improve their work without teacher intervention, the more they become independent learners and genuine practitioners of science. Sometimes students don’t notice (or were first to post their prediction), so I will occasionally ask a group to go up to the track and compare their prediction with the others.



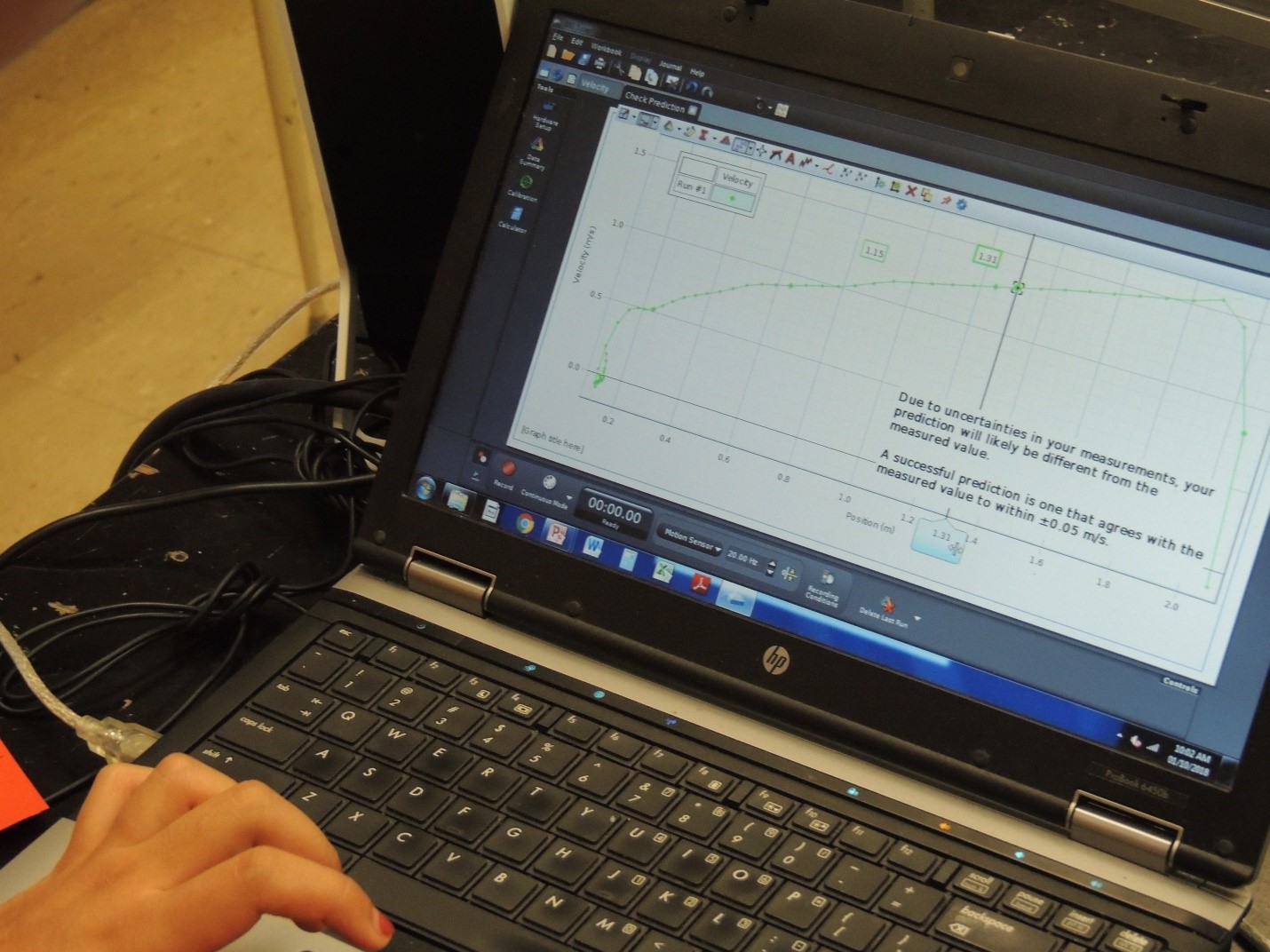
When all the predictions are in, I invite the groups to use the computer to check their prediction, giving them an uncertainty of ± 0.05 m/s. The computer shows a graph of velocity vs. position, allowing for a quick check. We very purposefully use the word prediction and I ask them whether their prediction agrees with the measured value. This is how scientists think and discuss their work: if you are not collecting data, pretty much every calculation you make in physics is a prediction based on a model with a set of assumptions. This is the vocabulary and conceptual framework we use in grade 11.

Students recognize that this process encourages a different way of thinking. Here is another response from my recent motion test: 



Result: Students feel like they are doing something real and meaningful. There is a lot of careful thinking required to set up the problem, part A of our solution process. Most experts spend a majority of their time defining a novel problem; this provides students with a chance to experience this. Students really enjoy seeing how their prediction fits in with the others and get a real kick when it agrees with the computer’s data (99% of the time). And if it doesn’t, it’s not a teacher saying “you’re wrong”; it is data that is suggesting you need to take another look at your work.

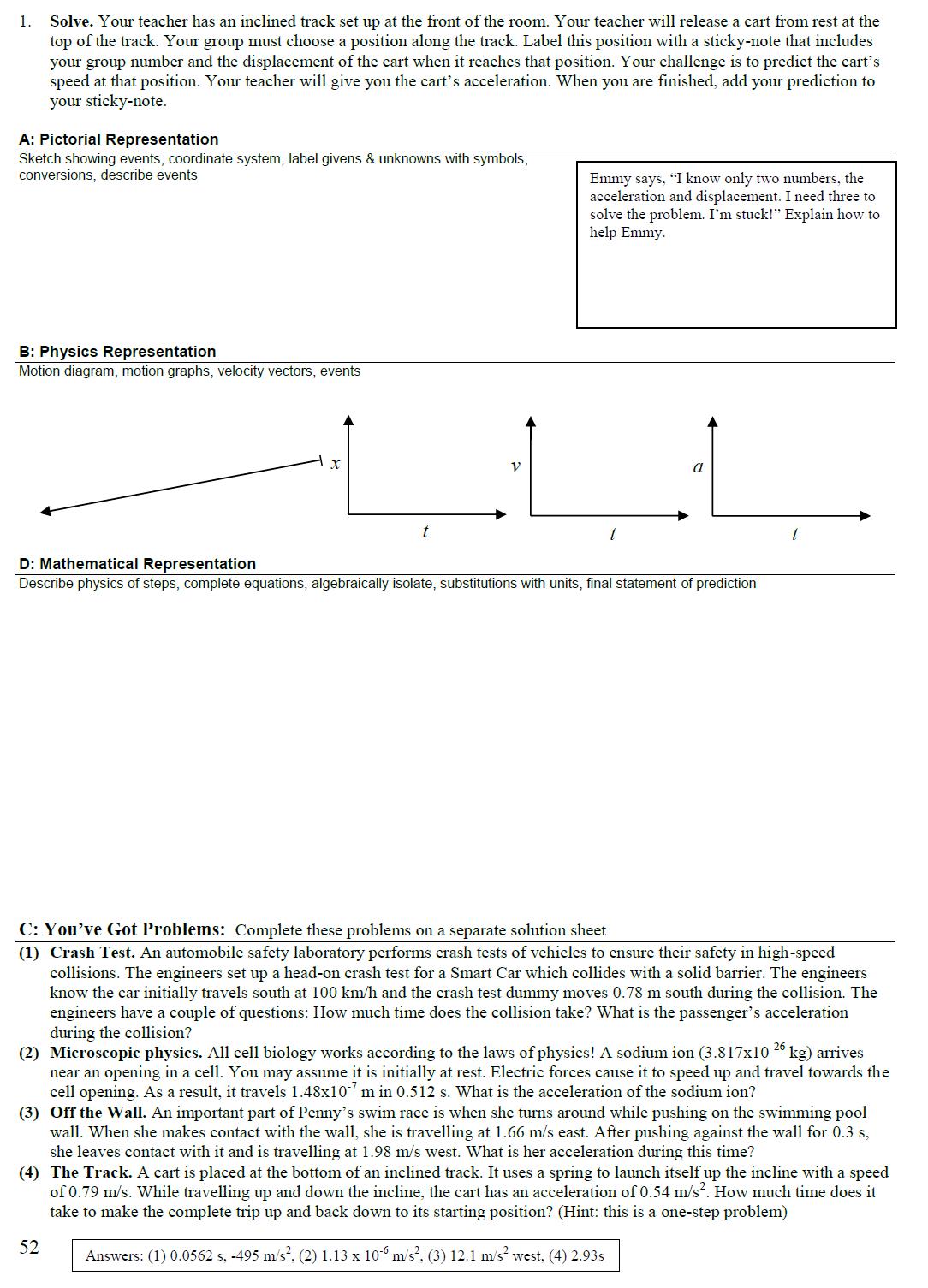
The full investigation is shown below. You can download the complete set of resources here. Enjoy!

Tags: Kinematics, Motion, Pedagogy