Kelly Foyle (kfoyle@perimeterinstitute.ca), Outreach Scientist, Perimeter Institute for Theoretical Physics
Philip Freeman (freeman@sphericalcows.net), Teacher, sd38 (Richmond) Richmond, BC

The authors were inspired to write this article while they worked on Perimeter Institute’s new black hole resource together. To learn more about general relativity and black holes and find ready-to-use, hands-on activities you can do with your class, download the free resource here.

One of the most startling and remarkable discoveries of the 20^th century was that gravity is not a mysterious, invisible force. In developing general relativity, Einstein showed that gravity is the curvature of spacetime due to the presence of mass and energy. But what does the “curvature of spacetime” mean? It is hard to get your head around this mind-bending concept! In relativity, space and time are mixed together into “spacetime” and gravity is explained by the curved geometry of this combination. That space and time can be mixed and curved is contradictory to all our everyday experiences. It is a lot for our brains to handle. While physicists can use the equations, even they need to use analogies to build a deep understanding of such counterintuitive concepts.

One common analogy used to introduce general relativity is the idea of a “mass on a rubber sheet” or “bowling ball on a trampoline”. The bending of the surface caused by the mass pulling the sheet down is used to illustrate the curvature of spacetime in general relativity. A rolling marble on the surface follows a curved path, or “orbits” the central mass, giving convincing evidence of the parallel between the sheet and the action of gravity. But there is a problem with this demonstration – it isn’t showing what it claims to show. In this article we argue that this analogy, as used, is fundamentally flawed and creates significant misunderstanding for both students and teachers. We explain where the problems arise, and how to avoid these problems and still provide a strong visual model and deeper understanding of how general relativity works.

We all use analogies ― they give our brains a break and make the unknown seem more familiar. If you’ve never seen a giraffe, being told that it is like a long-necked horse is pretty helpful. But analogies are also dangerous because they are inherently wrong. A giraffe is like a horse in some ways, but it is different from a horse in many important ways. Without explicitly stating the limitations and boundaries of the analogy, the risk is that it is overextended, and misconceptions are introduced. Many misunderstandings about physics in general, and modern physics in particular, come from overextended or poorly chosen analogies.

The bowling ball and trampoline analogy
One of the most popular ways to demonstrate gravity in the context of general relativity is to show a trampoline (or sheet of fabric) sagging due to the presence of a heavy mass like a bowling ball (see Figure 1). The trampoline is supposed to represent spacetime and the sagging the curvature of spacetime caused by the mass of the bowling ball. Typically, we roll marbles across the surface and watch how the fabric deflects the paths of the marbles. We are then told that the curvature of the sheet explains the deflection and therefore explains gravity in the general relativistic context.


Figure 1. A popular way to demonstrate general relativity is to have students roll marbles across a sheet that has been deformed by a mass. Some demonstrations found online such as this one have over 60 million views. While demonstrations like this are fun, we argue educators should not use them as models for general relativity.

The bowling-ball-trampoline analogy has several problems, some of which are shown in the xkcd cartoon in Figure 2. First, what causes the fabric to sag? The massive ball at the centre of the fabric is being pulled down, but by what? For many students this is a real confusion because gravity in the analogy is being caused by gravity outside the analogy. We are explaining gravity using gravity.


Figure 2 Explaining general relativity with a Newtonian description of gravity is basically explaining gravity with gravity. The tautology can only lead to confusion! Illustration: xkcd.com (https://xkcd.com/895/) used under a Creative Commons license.

Second, why does the marble roll down into the well? Because it is being accelerated by the Earth’s gravity and the force from the fabric (see Figure 3). It deflects or “orbits” because of the acceleration caused by these forces, and ultimately because the shape of the fabric creates a potential well. This use of a bent fabric is in fact a demonstration of force and potential, not of the effect of geometry.


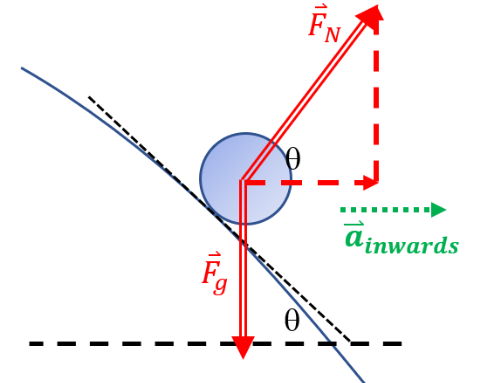Figure 3. A marble rolling on a trampoline experiences a normal force from the surface of the trampoline. This means that the slope of the fabric results in a force with a component towards the centre of the depression, giving the marble an inwards acceleration. But general relativity is not about forces or acceleration! The marble rolling on a trampoline analogy is a good analogy for Newtonian gravity, but not for general relativity. Illustration: P. Freeman

General relativity is a geometric theory and not a theory of forces. General relativity holds that the path of an object moving near another massive object appears deflected but is in fact following the shortest path (called a geodesic) with no force acting and no acceleration. The geometry of spacetime causes this straightest possible line to appear curved compared to expectations of our usual flat geometry.

What is curvature?
The fact that the shortest path between two points appears curved is the result of the mathematical property known, quite reasonably, as curvature. Curvature is the deviation from certain rules of Euclidean geometry. We can see it in many ways: initially parallel lines diverge or converge when extended, the interior angles of a triangle add up to something other than 180°, the area of a circle is not π times the radius squared, the circumference of a circle is different than 2πr and so on.

Ultimately this difference results from the distance between points on the surface having a different relationship than the one we usually take for granted, so that it no longer follows the same geometric rules. We see such changes when we try to make three-dimensional surfaces match with our familiar two-dimensional plane. Anyone who has done any sewing of clothing knows that making flat fabric fit a human body is not trivial. The various notches and gussets of a pattern are necessary because of curvature. Similarly, airplane routes along ‘great circle’ paths look like massive detours on a flat map but are indeed the shortest route possible.

In a demonstration of general relativity, trajectories should curve because they are following the shortest paths in a space with curvature and this can be shown with the bowling-ball-trampoline analogy. We can illustrate a “straightest line” path on the trampoline by laying down a strip of tape so it is as flat as possible. Any deviation from the “straight” (or shortest) path will wrinkle the tape. Figure 4 illustrates some of the geometrical effects caused by the curvature of a sheet of fabric similar to the trampoline. The triangle is made with straight lines using tape, and the circle is traced using a pin and a string to establish constant radius. You can see how the changes in distances caused by the curvature of the fabric cause the geometry to differ from our “Euclidean” expectations. However, this is the extent of the accuracy of the analogy.


Figure 4. A sagging sheet like a trampoline does indeed create a surface with curvature, as shown by the measurements of the angles in a triangle and the circumference of a circle. Seen from above (a) we observe a 2-D surface with non-Euclidean geometry. A view from the side shows why the geometry is different because of the bending into a third dimension. This is why the sagging trampoline does illustrate curvature, but rolling marbles on the surface involves different effects altogether. Photograph: Philip Freeman

The origins of the trampoline analogy
The roots of the bowling-ball-trampoline analogy come from a popular visualization tool used by physicists called an embedding diagram.

Even the brains of physicists who have been studying general relativity for years can’t handle visualizing three dimensions of space mixed with time all acting in a non-Euclidean way (you are not alone!). To simplify it they sometimes remove time completely and also remove one dimension of space.

An embedding diagram shows how a slice of 2-D space (a plane) is curved in general relativity by embedding the slice in a make-believe third dimension. Figure 4 is an illustration of exactly that. The 2-D surface (the fabric) is embedded and bent into a 3-D space (the surrounding room). What we often neglect to say is that the 2-D surface is typically a slice through the equator of the massive object causing the curvature. Figure 5 shows such a slice through a massive object such as a star or a planet. The surface in such a diagram has geometry that is no longer ‘flat’ — the circumference of a circle is not equal to 2πr, and the other rules of geometry also are changed. The bending of the surface in the make-believe dimension causes it to have curvature in a way we can understand. Although curvature in general relativity does not actually involve an extra dimension like this, embedding diagrams are useful to visualize that there is more space than we might expect due to spacetime curvature. The fact that there is more space near massive objects has in fact been measured by the Cassini probe to Saturn. A signal sent from Cassini to Earth that passed near the Sun took longer to reach us than expected because the signal had to travel through more space due to the curvature caused by the presence of the Sun.


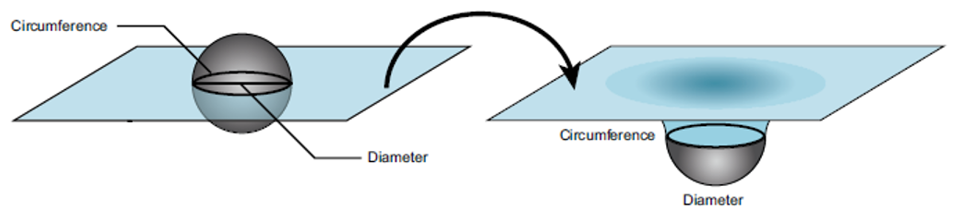Figure 5. Physicists use an embedding diagram to visualize curvature of a 2-D slice of space at the equator of a massive object. Illustration: Dee Panetta from Perimeter Institute’s Black Holes (2020) resource

Looking at Figure 5 it is easy to see where the idea of a sagging trampoline originates. Unfortunately, the analogy has been overextended. While it is true that a piece of tape following a straightest path will appear curved, rolling marbles on the surface is an overextension that leads to misconceptions. The path of a marble on a sagging trampoline is bent by forces and not by curvature of the fabric. Such demonstrations are fundamentally flawed to illustrate general relativity (though there are productive ways of using them to illustrate Newtonian gravity).
Can we ‘fix’ this analogy to help understand general relativity?

A good analogy for general relativity should rely on curvature, not on a Newtonian description of gravity through forces. When illustrating curvature in general relativity, you can bend the fabric up or down (as shown in Figure 6).


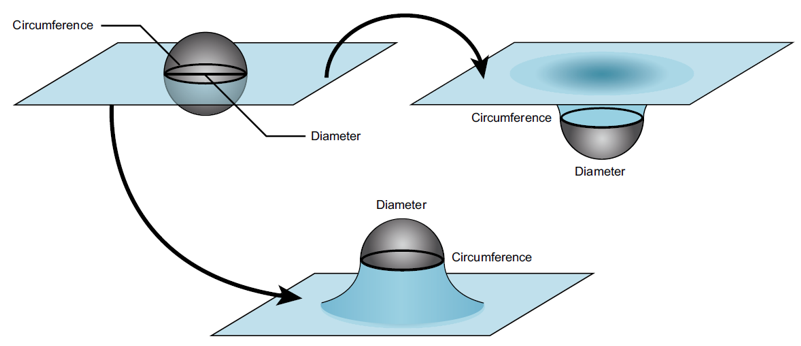Figure 6. To help visualize the curvature of space in general relativity, physicists restrict themselves to a 2-D slice of space at the equator of a massive object (upper left). Imagining this sheet as being bent in a make-believe extra dimension produces the effects of curvature. You could bend the sheet downward (upper right), but the curvature can also be illustrated by bending it upward (lower) because it is the changes in distances and amount of space within a region that cause the curvature, and not the bending itself. Illustration: Dee Panetta from Perimeter Institute’s Black Holes (2020) resource

Either way you bend the fabric the same curvature is created, and all the effects on geometry are the same. Rather than bending the fabric down using a massive object placed at its centre, if you bend the fabric up you remove the confusing role of Earth’s gravity causing the bending and the misleading effects of the forces from gravity and the surface. To bend the fabric up, you can place a support like a flask or funnel with a marble on top beneath the fabric as shown in Figure 7.


Figure 7. Bending the fabric up still shows the effects of curvature but doesn’t use Newtonian gravity to cause the curving. Green tape illustrates the path an object would take on this 2-D slice of space. The photo on the left is taken from above and shows the path as seen in space. The photo on the right is taken from an angle and shows the displacement in the make-believe embedding dimension that produces the curvature in the model. Photograph: Philip Freeman

Placing strips of tape illustrates how straight paths become bent by curved space. The upward bent fabric and the downward bent fabric have exactly the same curvature — but opposite slopes. This is why a piece of tape illustrating the “straightest line” path will curve the same way in both cases, but a rolling marble will behave quite differently. The path of the tape is deflected due to the curvature of the fabric whereas the marble is accelerated by forces caused by the slope of the fabric. A slope creates a force on an object placed on it which brings us back to Newton’s explanation of gravity. General relativity, however, does not involve force at all. Bending the fabric up and using tape to illustrate the effects of curved space and allows you to use the powerful hands-on experience of the fabric without conflating these two understandings of gravity.

What are the limitations?
Every analogy has its limits and it is important to know and share those limitations when we use the analogy.

Probably the most obvious, of course, is that space isn’t a two-dimensional piece of fabric! A surprising number of people take this analogy literally, so be aware of this risk.

Another limitation is the fabric model leaves out more than just one spatial dimension. Bending fabric up is a great way to illustrate the curvature of a 2-D slice of space. In Figure 7 we can see that the curvature causes the straightest line path going past a gravitational source to curve, but it doesn’t show why different objects moving past that source would bend differently. There is only one way to lay down the tape after all! And how do you put down the tape for a stationary object?

The problem is that this embedding does not show us how spacetime is warped. Time has been completely removed from the analogy. General relativity predicts warping effects on time that are similar to those on space, and even more pronounced in their effect. Objects at rest or moving differently are following different paths in this combined spacetime.

One of Einstein’s key insights is that we can’t speak of space and time separately. The two are forever intertwined as “spacetime.” General relativity requires considering the path of an object in both space and time and to visualize the warping of “space” and “time,” spacetime diagrams are essential.

Let’s explore how spacetime diagrams can help to show differences in spacetime paths by considering three balls at the top of a cliff. One ball is dropped from rest and the other two are launched horizontally from the same location at the same time, but with different speeds (see Figure 8). Both launched balls will initially travel along the same path but will soon diverge. The faster ball will travel farther than the slower one before striking the ground. The dropped ball accelerates without any motion in the x-direction at all. In our usual Newtonian model we can explain this all very easily using a force that causes an acceleration, and map out the trajectories (a space-space diagram if you like):


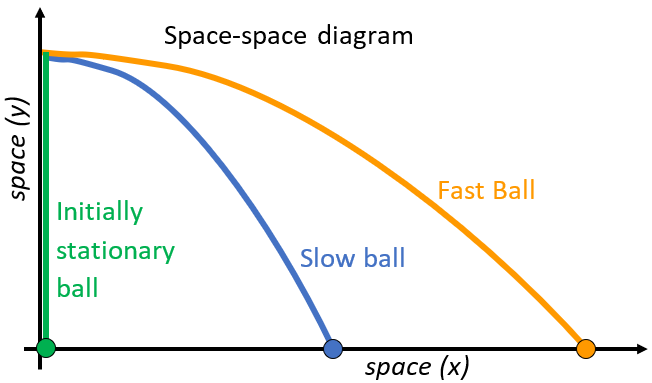Figure 8. Both the slow and fast ball start on the same path as they move horizontally. However, their paths soon diverge and the fast ball travels further than the slow one. Curving space alone cannot explain this behavior. The initially stationary ball falls, even though it has no direction of motion to start with at all. Illustration: Kelly Foyle and Philip Freeman

While this is familiar to us, it is not easily explained using tape on stretchy fabric the way we showed. Since the two moving balls are launched from the same location and in the same direction, we would represent them with pieces of tape starting in the same direction, and thus we would expect the balls to travel along the same path, which we know is not the case! And a stationary ball doesn’t follow any path, never mind a curve, but it is clearly affected by gravity.

What is missing from the tape and fabric analogy? The warping of time!
To show the effects of curvature on time we need to use a graph that includes both space and time (a “spacetime” diagram). Figure 9 shows the spacetime graph for the three balls, focusing on the x-direction. Notice that we are no longer showing the y-spatial dimension and are instead showing time on the vertical axis. This means only the x-component of the balls’ motion is shown. The initially stationary ball doesn’t change its x-position, so it is shown by a straight line going up (same place at different times). The other two balls don’t accelerate in the x-direction, so they pass through equal amounts of space (in the x-direction) in equal amounts of time, making the spacetime path a straight line. The faster ball passes through more space in the same amount of time, so its path is less steep (in this kind of diagram the speed is the inverse of the slope of the lines). Notice that although the two thrown balls traveled in the same direction in space, they did not travel the same direction in spacetime. For two objects to travel the same path in a spacetime diagram they would need to travel at the same speed.


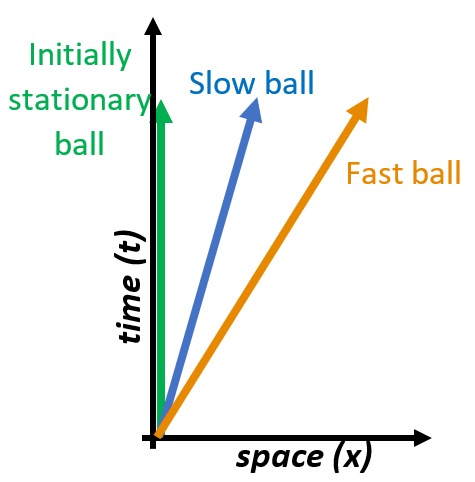Figure 9. In a spacetime diagram time is usually plotted on the vertical axis. This means only the x-component of space is being shown. Unlike a demonstration using tape and fabric, a spacetime diagram shows that the balls all move in different directions in spacetime, and do not follow the same path. Illustration: Kelly Foyle and Philip Freeman

Even an object at rest is moving through time. This is why gravity is still apparent even when you are not moving through space. You are always moving through time, and thus the curvature of spacetime can explain gravity.

This is also shown in Figure 10, showing an object falling from rest. Notice the similarity between the path of the initially stationary object through spacetime and the lines made with tape on the curved surface of the fabric model in Figure 7. An object that begins at rest (constant position = a vertical line on the spacetime diagram): does not keep that direction. As it follows its ‘straightest line’ in curved spacetime it appears to bend, causing it to move faster and faster (it is falling!).


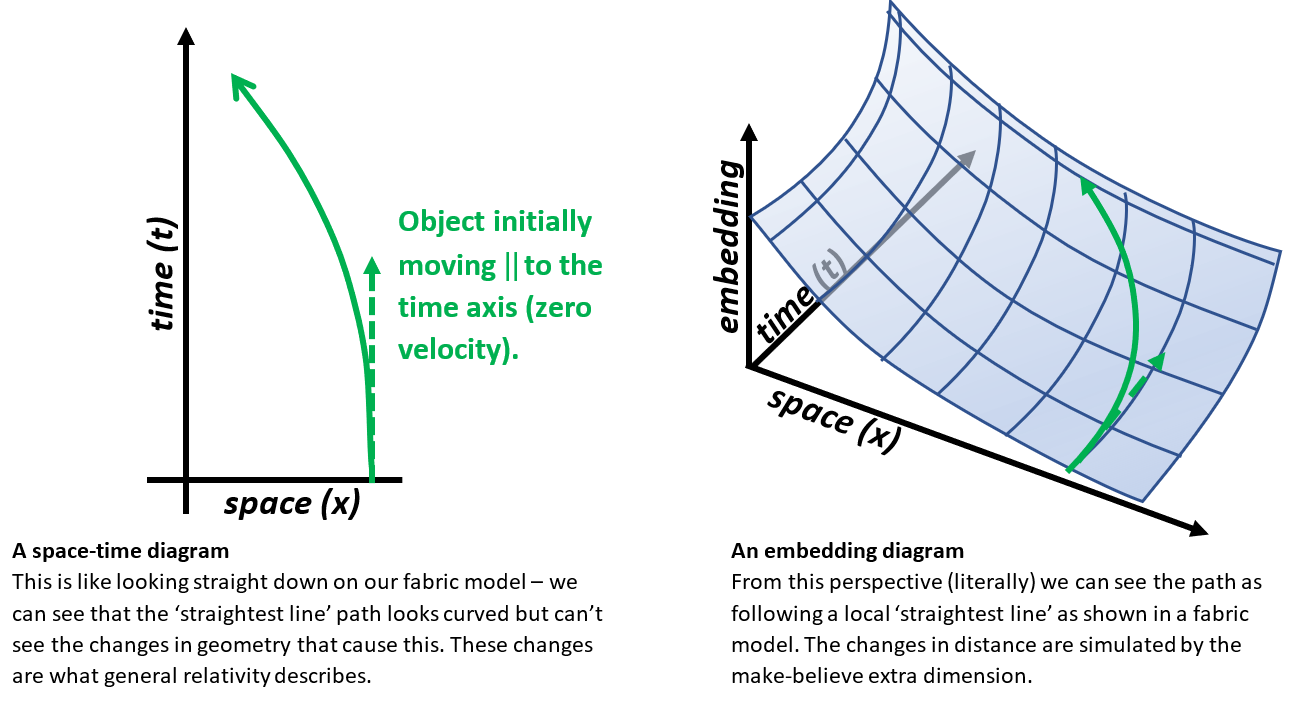Figure 10. How spacetime curvature affects the motion of a particle as it moves through time. Note the similarity to the shortest paths shown by the tape on our bent fabric earlier (see Figure 7). Illustration: Philip Freeman

In order to continue to stay in one place and not follow the ‘curved’ straightest path (i.e. in order not to fall) we would need to exert a force to keep the object’s path in spacetime vertical (i.e. at a constant position). This could be, for example, a force such as the one your chair is exerting on you as you read this! The chair is constantly pushing you away from a straightest line path through spacetime. Setting aside air friction, a falling object experiences no forces at all and follows a straightest line path through curved spacetime. This is how general relativity uses the curvature of spacetime to explain gravity.

We said we could measure the “warping of space” in terms of the amount of space measured “inside” a region. Is there something similar that shows what we mean by “warping of time”? Such a warping of time implies a different amount of time within a region — the rate at which clocks run changes with distance from a massive body. This is observed to be true and extremely well-tested.
In fact, almost all our everyday experiences of gravity (i.e. throwing a ball or being stuck to the Earth) are due to the warping of time in general relativity and not the warping of space. The warping of time gives us essentially Newton’s gravity, while the effect of curvature of space is quite small and makes a difference only in extreme cases, such as the discrepancy in the precession of Mercury’s orbit.

What should an educator do?
First acknowledge that understanding general relativity is difficult because it is not intuitive. Human beings are limited by their senses and it is not possible for us to visualize three dimensions of space and time mixed together. The only way for our brains to make sense of it is to visualize parts of it, but not the whole thing all at once. We need to be aware of the limitations of analogies and not make overextensions (i.e. rolling marbles).

Second, have students explore a demonstration of the stretchy fabric in the ‘bent up’ orientation. Discuss how the curvature of space deflects the paths on the surface of the fabric, in contrast to the force description of Newtonian gravity.

Third, explicitly state the limitations of the analogy ― only two dimensions of space are being shown and time is being completely ignored. Also, the fabric is being bent into a make-believe dimension that doesn’t exist but helps us visualize curvature. Curvature does not actually require such an extra dimension.

Finally, if time permits, introduce an alternative visualization — the spacetime diagram. This visualization is also limited in that it only shows one or two dimensions of space, but it can help us better comprehend the effects through time, which produce gravity as we usually experience it.

For more information and hands-on activities for students, download Perimeter Institute’s new Black Hole resource.

Tags: Modern Physics