Chris Meyer, Past President, Ontario Association of Physics Teachers
chris_meyer1@sympatico.ca

In my early years of teaching physics, I was often surprised by the difficulties my grade 12 students (actually OAC students at the time!) had with forces. Many times, the sneaky culprit responsible for their troubles was the first law of motion. “Why are they having trouble with such simple grade 11 ideas?” I puzzled, “these are good students”. I have been wrestling with this question for 23 years and now have a better understanding of what I'm trying to accomplish as a teacher and what is happening inside my students’ heads. Let’s explore a better way to train students to think about forces.

Setting examples for everyone
My first attempt to solve this problem was to provide more examples for the first law of motion: fun examples like pulling the tablecloth out from under the dishes, and pedagogical examples so they could practice using the first law. I was a firm adherent of the idea: “you just need to try enough examples and then you'll get it” - we’ve all seen how things sometimes just “click” with some practice. But here is the problem with that approach: it relies on luck and happenstance, wasting a lot of time, energy, and student enthusiasm. For many students, the “click” either doesn't happen at the right time or doesn’t happen at all. We want learning physics to be both quick and reliable, so students have the skills they need to progress. This requires us to unpack the thinking processes that experts use and provide students with deliberate practice of those processes under careful supervision. This is the idea behind the pedagogical theory of cognitive apprenticeship: we are training students in cognitive tasks that often happen invisibly; these tasks need to be identified, systematized, taught, and practiced under expert guidance.

A look under the cognitive hood
So rather than being teachers of physics, we should be teachers of thinking processes that happen to focus on physics. But of course, we all want to teach our students to become good thinkers, that's nothing new! What is new is how we approach this challenge using knowledge of how our brains work: how we think, store, and process information. The cognitive system that we sort through ideas with is our working memory. This system allows us to temporarily store some pieces of information while others are being processed or recalled. The famous rule of “7 plus or minus 2” describes its capacity: we can hold roughly 7 units of information in our working memory, depending on their complexity and familiarity. Much of what our physics students work with is complex and unfamiliar, at least at first, which places a heavy demand on their cognitive resources. Luckily, our brains have a workaround for this memory capacity limit: the psychological process of chunking.

Making physics chunks
At first glance, a complex piece of information like a set of numbers might seem challenging to remember, like: 02041974. But if we can break up this number into pieces that we recognize and make sense of, we can store the long number in our working memory in a more efficient way. Instead of storing 8 numerical digits, which is right at our working memory limit, a bit of training helps us to store it as a date: February 4^th 1974, now only three units of information. Information in our brain is stored relationally as a web of connections and not as discrete facts, so there can be a complex hierarchy of units that make this process even more efficient. For me, this string of eight digits is one unit of information, my birthday (no presents, please). The challenge for chunking in physics instruction is to break down complex concepts and processes into pieces that are easy to recognize, interpret, and make sense of.

Language is everything
Human thought works through language, which defines or limits what we think about and how we think about it (what a doubleplusgood idea!). And because knowledge is stored relationally in a complex web of connections, our understanding does not become clear until we access that web and construct our thoughts in language. This explains a common experience: we feel we understand something but find ourselves perplexed once we are challenged to speak or write about it (How many times has this happened to you in front of a class? For me, many!). Furthermore, the language commonly used to describe physics and forces can be unclear, inconsistent, or inefficient for the purposes of learning. Well-chosen labels for chunks can act as useful cognitive handholds that guide thinking through complex processes. Let’s take a tour through the language I use to describe forces and chunk its concepts.

Interactions. An interaction is a physical concept that is more fundamental than forces. For example, when two objects interact, they exert forces on one another. This helps to prepare students for thinking about forces and provides a physical explanation for the presence of a force at a particular moment in time.

Third-law force pairs. An interaction gives rise to a pair of forces that share an important set of properties described by the third law of motion. The label “third-law force pair” helps to keep the origin of the forces (a particular interaction) and their properties (the third law) front and center in our mind. It is also really helpful when talking about multiple objects interacting: “Which forces form a third-law pair?” is a nice, succinct question that is useful to ask.

State of force. The idea of a “state of motion” is a familiar one, but we were lacking a parallel term for force. In our exploration of states of force, my students work out that there are in fact only two: a state of balanced forces and a state of unbalanced forces. One can ask the general question, “when do the forces change?”, or the very specific question, “when does the state of force change?” It is a handy term!

System. This is an excellent term for labeling the “things we are interested in”, or a bit more technically, the “things whose properties we are keeping track of”. If we don't use this term, we often confuse or lose track of our objects of interest, leading to all sorts of problems, usually bad.

Net force expression. This is an algebraic statement using force symbols that gives the sum of the forces in a particular direction: F_net•y = F_t – F_g

Second law expressions. This refers to the component expressions for the second law of motion in the x and y-directions, cueing a writing process: start with the original expression (F_net•x = ma_x), replace the net force symbol with a net force expression (F_t – F_f = ma_x), and then substitute any zeros (F_t – F_f = 0).

Mass. Yes indeed, if you are ever tempted to say the word “inertia”, don’t! There is no situation at the introductory level where using the i-word clarifies anything. If you are actually referring to mass, just say “mass”! And really don't ever say that something happens “because of inertia”; in the framework we develop for introductory physics, we say that things happen because of forces, or a lack thereof.

System mass. This is a refinement to the mass term that appears in the second law of motion. It is a useful reminder that the symbol “m” refers to the mass of the entire system that we are considering. Lots of errors in thinking and in problem solving are due to a careless definition of this “m”.

Force diagram. Call things what they are and as clearly as possible. The phrase “free body diagram” likely has little meaning for students (and teachers!) and meaning is what makes the chunking process work.

Cognitive chaining things together
When we take chunks and join them together in a sequence, we form a cognitive chain of ideas that can outline a process. As the chain becomes well-practiced, the chain itself can become just another chunk in a larger chain (remember, knowledge is hierarchical). Chains help students work efficiently with procedural knowledge because a complex set of steps can be held as one chunk in working memory while the links within a chunk are easily recalled. One “simple” chain is the first law of motion. The traditional expression of this law hinders learning and does not clearly model the thinking processes we want students to practice. As an alternative, let's take a look at an example from the third lesson of my force unit where we develop the first law. We have just performed a series of experiments observing different states of force and their corresponding states of motion; now students are ready to identify patterns. The results at first seem complex but become organized and begin to form chunks as they are examined in the chart below.



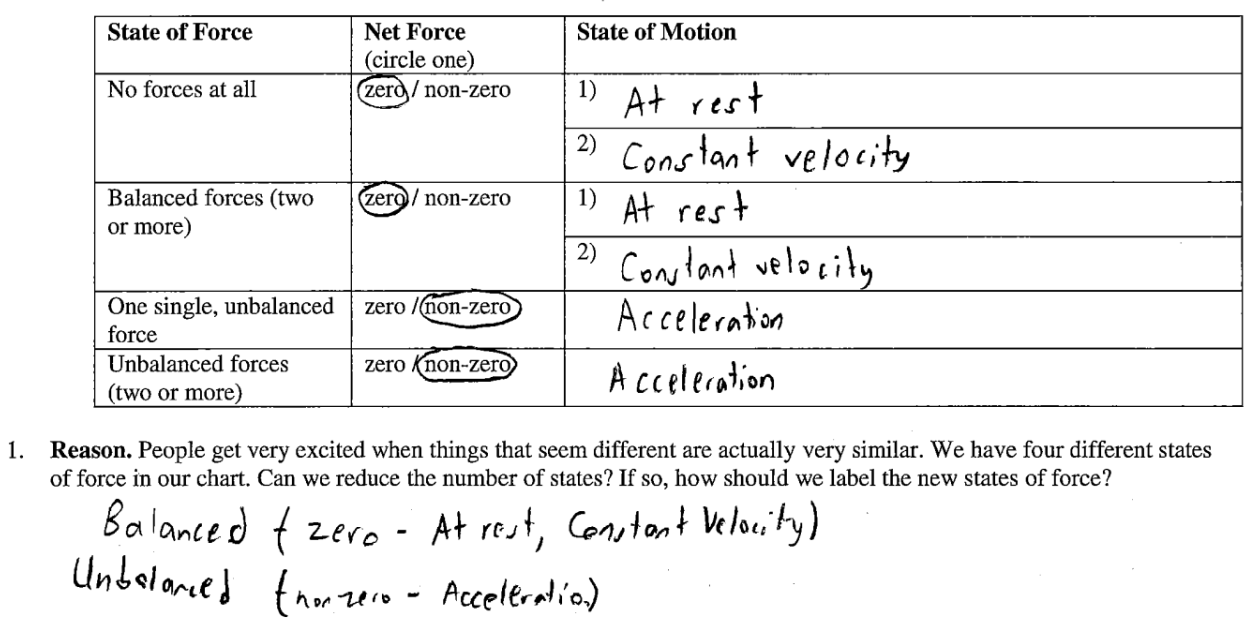
The force situations condense into two states: balanced forces and unbalanced forces. Likewise with motion: three motion situations reduce into two states of motion. The elegance of the first law becomes clear when it is phrased as connecting states of motion with states of force; the parallelism in language reinforces the idea of connection. And so, we have formed a cognitive chain that becomes a well-rehearsed thinking process: “if we have this state of motion then we also have this state of force” or vice versa. This formulation of the first law has no pithy statement. This approach shows the first law for what it is, a cognitive process that connects states of motion with states of force. Also notice that the pernicious word “inertia” is nowhere to be seen!

Training in chaining
An important feature of the chaining strategy is that skills, even new ones, are never practiced in isolation; they are always linked to other skills or ideas. After completing the first law chart above, students tackle the following practice. Notice how each example involves a sequence of skills.



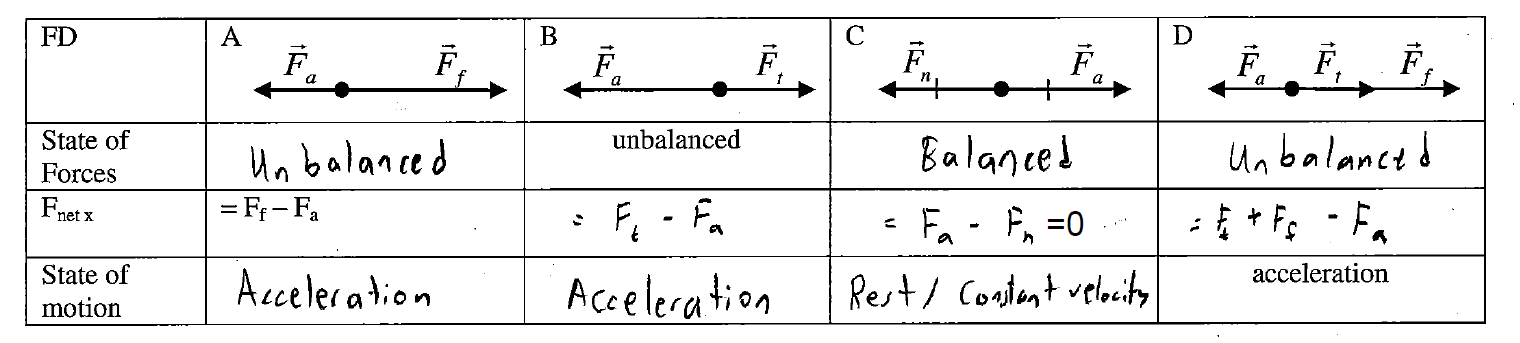Extending the chain
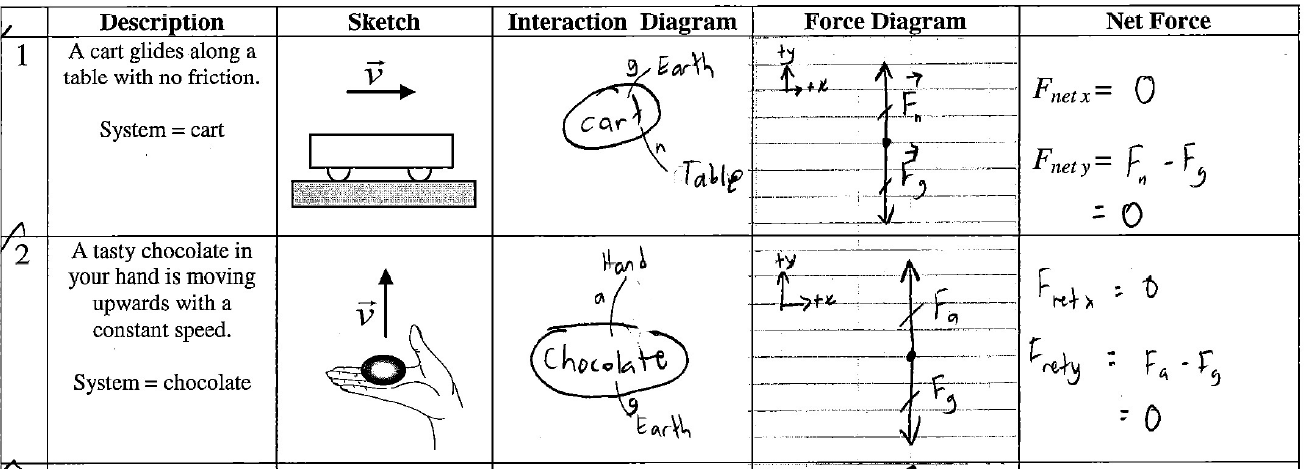
As we progress through the first six lessons of the grade 11 force unit, we develop more chunks of force concepts and link them into longer chains. The links are repeatedly reinforced in structured ways that make the thinking process visible and allow students explicit practice. Here is an exercise from the homework that provides students’ first opportunity to draw a force diagram “from scratch”.



In this example we are given a description of a situation and we would like to construct a force diagram. The required steps in the force thinking process, which are the elements of our cognitive chain, are shown as items in the row of a chart. We begin with the interaction diagram, where we define a system and identify the important interactions between system objects and the environment. The interaction diagram is its own cognitive chain, but now appears as a chunk (not familiar with an interaction diagram? Learn more!). The organization of the chart leads students through the correct sequence of reasoning to the state of motion and then to the state of force. Once these have been decided, students can draw a force diagram with vectors of the appropriate relative length to visually represent the state of force in each direction. Our chain is getting longer! It's funny to think that in the past, I gave tasks like these (draw a force diagram) with none of this structure. And sure enough, students drew arrow-pricked monstrosities — they were just winging it and guessing at the forces (But if they just try enough examples, surely…).

Linking to kinematics
In the lesson that follows the construction of the first law, we explore what happens when the state of force changes: an oft neglected aspect of the first law. The focus is an experiment where a cart accelerates due to a falling weight and the weight strikes the ground, causing the state of force to change while the cart continues to move. Here is the chart from this lesson outlining the force thinking process:



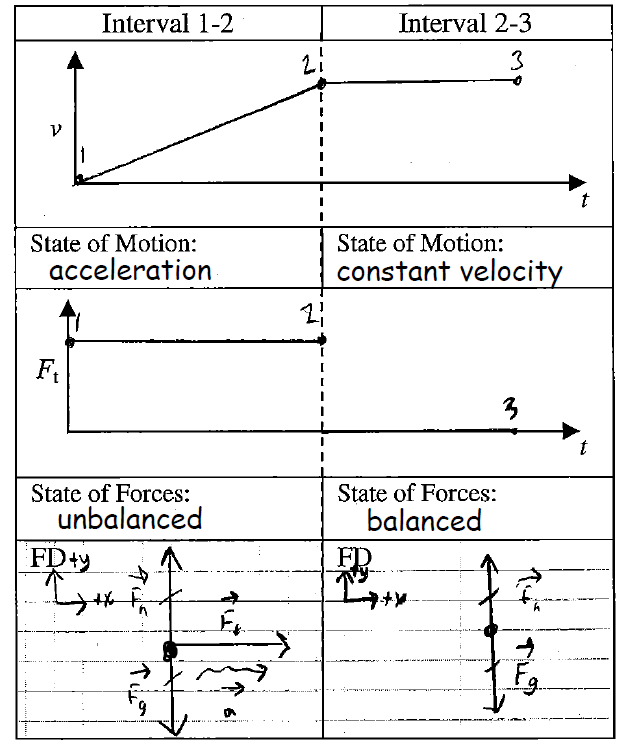
The vertical orientation of this chart helps to line up the thinking process with time intervals shown in the velocity graph; the interaction diagram was completed earlier in the lesson. Now motion graphs, which can provide experimental evidence for the state of motion, are linked to our force thinking process! Note that this particular investigation also helps tackle a very challenging idea: an object can be moving even when it experiences a state of balanced forces.

The homework for this lesson is a good workout for our growing cognitive chain. In this example, spanning multiple intervals of time, students work backwards from a force understanding to construct a velocity graph. There is enough subtlety in this example that students can’t reliably describe the motion before thinking carefully about the forces!



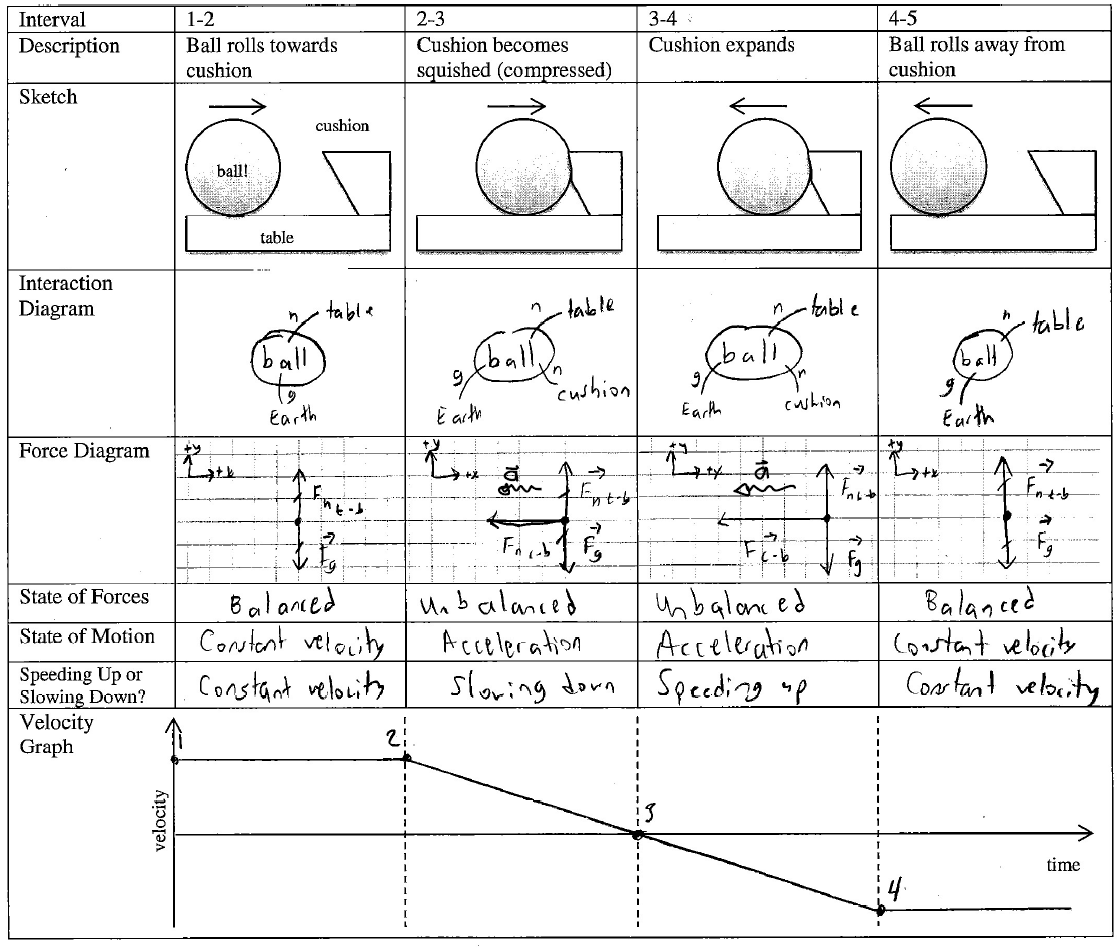
Note that students are instructed to assume that there is no friction in this example and they automatically assume the forces are constant (which is okay for our purposes) during each interval.

Connecting to the second law
As students improve their fluency in this cognitive chain, we begin to leave out prompts for steps that begin to happen automatically. Pedagogically, we are changing our scaffolding due to students’ changing zone of proximal development.



In this set of homework exercises, the explicit work with the first law is left out while the net force expressions that connect with the second law of motion are added (note that this isn’t the full second law yet, we are getting there!).

The full chain for the force reasoning process
The full chain never appears in any one lesson or exercise, but it does appear on our rubric page, fleshed out and ready to help students if they get stuck. The chain is represented with links that point in each direction. As a result, one could start at any point within the chain and work backwards or forwards depending on the goals of the thinking process. In a schematic way, this represents the flexibility and the efficiency of expert force thinking.



Each step in this process represents a complex hierarchy of ideas and skills, all of which are easier to internalize and retrieve due to their careful introduction, categorization, and meaningful labels — they are well chunked! The culmination of this work happens when we tackle second law problem solving where the whole force thinking process is inserted into our rich problem-solving framework. The solution structure you see below is always given when we ask students to solve force problems for homework or on tests.





As a bonus, you can see the corrections that my student has written in blue to her work. This was a practice test where students wrote their own feedback. Also, our grade 11 forces test always includes a question like this one where the forces change, which requires a deeper understanding of the first law.

Begin the cognitive apprenticeship
We want our students to be successful in physics, but traditional strategies like the “just try more examples!” gambit are inefficient and haphazard. By focusing our teaching efforts on the thinking processes that experts use, our students can learn faster and more consistently. The careful chunking and chaining of physics ideas reduces the cognitive burden on our students, allowing them to tackle more interesting and nuanced physics tasks while having a more satisfying learning experience. I hope you are left with the impression that all of this is quite reasonable and maybe even obvious! In retrospect, it seems strange that it took me over 20 years of hard work to get to this point. I'll take that as a sign of the subtlety and challenge in developing a cognitive apprenticeship for the understanding forces. If you are interested in learning more, please explore the entire force unit that I have created for grade 11 physics.

A final note: naming the three laws of motion
Throughout this article I have been referring to what are often called “Newton’s laws of motion” as “the three laws of motion”. Did you notice this? I do this for two reasons. First, these laws represent the work of many thinkers prior to Newton, as Newton himself acknowledged, and are a good example of Stigler’s Law of Eponymy. It is more historically accurate or fair to simply call them the “three laws of motion”. And second, these laws belong to all of us and not to one individual. Every time a student goes through the process of constructing an understanding of these laws, they become owners of these ideas; the laws become theirs, not just Newton’s. This takes the laws of motion out of the hands of one person, from one place long ago past, and helps them to become a part of each student who strives to learn them. The three laws of motion are an extraordinary part of our shared cultural inheritance as human beings who seek to make sense of the universe.

Tags: Forces, Pedagogy