Philip Freeman, teacher at Richmond Secondary School (Richmond BC), Executive member BCAPT
freeman@sphericalcows.net

Most short introductions to special relativity include the idea that the relativistic mass of an object depends on its velocity (m = γm₀). However, if you do much further reading in modern physics you will soon come across the idea that this is a bad concept. Why? What is wrong with the term ‘relativistic mass’? Some answers to this are physical, some ideological. Here is an overview of the case for and against relativistic mass.

Terms
One of the problems with talking about mass in this debate is that it is hard to even have the discussion when the terms involved, especially mass, are what is under debate. I will, for the purposes of this discussion, refer to the mass of an object in its own frame (which the one school wishes to call simply mass) as “rest mass” and the changing mass due to reference frame (which the first school wants to banish and the other school tends to call simply mass) as “relativistic mass”.

What’s wrong with relativistic mass?
The physical problem is that there is no unique way to define relativistic mass and get consistent results. The relativistic mass has to be treated very carefully or you will end up with odd concepts such as tangential mass vs. radial mass. How can mass have direction? For example, when calculating the bending of light as it goes past a large mass like the Sun, you might say that this light has a “relativistic mass” equal to E/c² and then use Newton’s formula to determine how gravity affects it. This will give you the right answer if the light is moving toward or away from the Sun, but it will give the wrong answer if you try to use it for light moving sideways past the Sun.
This gets even worse when we get to general relativity (as you might expect given the example above). In general relativity there is no unique consistent way to define mass at all. In many special circumstances there are useful versions of mass, but different ones for different circumstances (ADM mass for asymptotically flat spacetimes, Komrar mass for static/stationary spacetimes, etc.) For now we will focus on special relativity.

Given how easily the concept of relativistic mass can lead to confusion, some physicists (especially particle physicists) have championed the idea that the term ‘mass’ should only mean ‘rest mass’.

Rest mass is a relativistic invariant (at least in special relativity) and in physics we generally seek invariant qualities as being in some sense ‘deeper’ than observer-dependent ones. It therefore makes sense to focus on this and avoid all that confusion. Thus these physicists conclude that that is what everyone should do.

But what is rest mass? This is a little tricky, because the mass viewed in this way is not a property of objects, but rather a property of systems. The rest mass is the mass of a system in its centre of mass frame. If the system as a whole is moving then its overall kinetic energy is not part of its rest mass, but the kinetic energy due to internal motion is part of the rest mass. This is analogous to the idea of internal energy in thermodynamics, where the overall kinetic energy of a system as a whole is not part of the internal energy, but the ‘hidden’ internal kinetic energy of the particles that make up the system is part of the internal energy.

What’s not wrong about relativistic mass?
The declaration that we should banish the term ‘relativistic mass’ is where the ‘political’ element of this debate manifests. Each perspective on the meaning of mass has its positive and negative aspects, and to argue that either one is the “one true way” is not really a scientific, or even a pedagogical, choice but an ideological one.

The idea that ‘only rest mass is mass’ is itself subject to misunderstandings and misconceptions. The rest mass is a property of a system, and what is considered relativistic mass within that system will appear to be part of the rest mass if you are outside of it. For instance, the rest mass of a globular cluster is the sum of the relativistic masses of the orbiting stars within the cluster. Similarly, the rest mass of a proton is a hundred times the rest mass of the quarks that it is ‘made of’ because the protons have vast amounts of stored energy in the fields and in the kinetic energy of those quarks, i.e. their relativistic mass. Thus in adopting a ‘mass means rest mass’ stance we gain observer independence for our definition of mass, but trade a different kind of universality for it.

So, for example, a system consisting of two masses both moving in the same direction has a different rest mass than a system consisting of those same two masses moving in opposite directions (note the similarity to the way in which mechanical energy and internal energy are dependent on how you think about a system!):
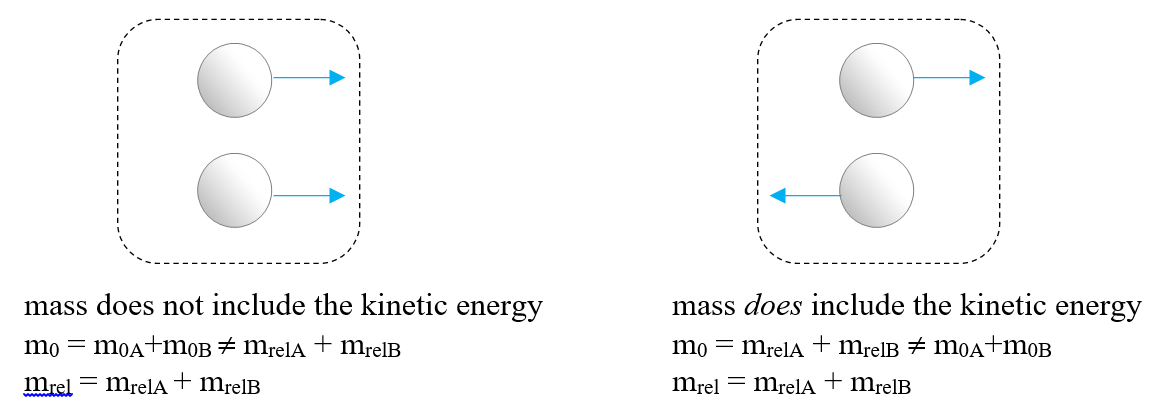 Figure 1: Rest mass of a system is not, in general, the sum or the rest masses of the parts of the system

Relativistic mass therefore preserves some of the features of mass we expect: it describes how difficult it is to change the motion of something and the mass of a system is equal to the mass of its parts. Neither of these features is preserved by the ‘mass means rest mass’ approach.

Let me give an example of a confusion I have encountered caused by the ‘mass = rest mass’ idea:
Some years ago a friend with an interest in physics came to me with a design for a ‘reactionless drive’. He knew something was wrong, but didn’t see what. The idea is this: take a long box with a photon source in one end and, say, a photocell at the other. Now have the photon source emit a pulse of light, or a single photon if you prefer. The light has momentum to the left, so the box will move to the right:


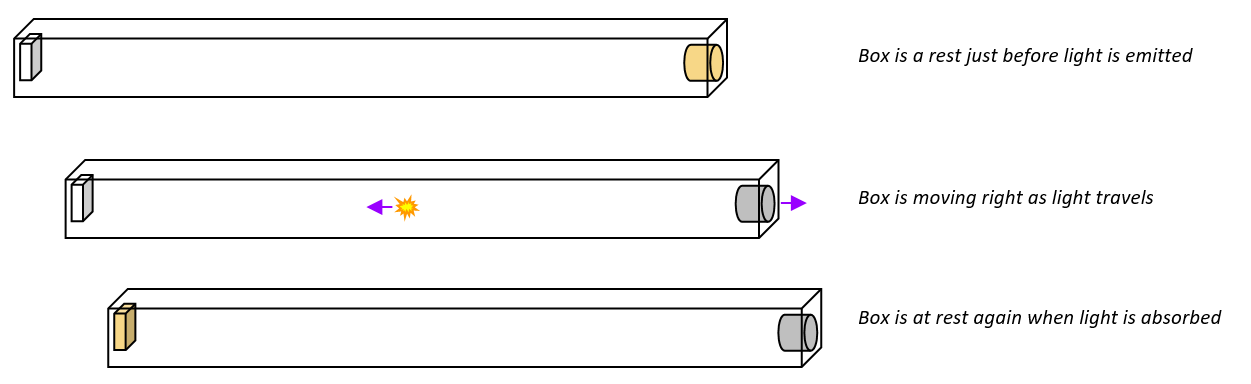Figure 2: Where is the centre of mass as the light is travelling?

Somehow as the light travels the box has moved without any apparent interaction with the outside world.

We can see that end of the box with the photocell is now ‘more massive’ than before and the other end ‘less massive’, because moving the energy has moved part of the mass, leaving the centre of mass in the same place… but if we have the ‘mass = rest mass” perspective it is hard to justify that without knowing what form the energy is in. Further while the light is travelling it unambiguously has no rest mass, so how can it be affecting the centre of mass?

The problem is that the light does have rest mass so long as we put the boundaries of the system around the box. But it doesn’t have rest mass if we put the boundaries just around the light and exclude the box. If ‘mass’ always means ‘rest mass’ then we have a bit of a mess here… it can be resolved in a view without relativistic mass, but only by dealing with complex and tricky definitions, and a high risk of confusion.

On the other hand, the box and light viewed with relativistic mass idea is much simpler… the centre of mass of the box never moves because as the light moves it carries energy which is part of the ‘relativistic mass’ of the system, and the situation is just like the classic example of a person walking towards the back of a boat in mechanics.

In further defense of the idea of relativistic mass, consider how length is handled. Rest or proper lengths are also invariant but few people advocate using the term ‘length’ to refer only to proper length. We are willing to accept that different frames measure length differently because we consider length to be the thing that measurement measures! If someone else measures a different length then length just isn’t the absolute thing we thought it was. In the same way we might opt to define mass as the thing we ‘measure’ in looking, for example, at the force needed to accelerate an object. And that is, observer dependent in much the same way that length is.

When E meets mc²:
To see the battle of definitions play out it is instructive to look at probably the best known, and therefore the most misunderstood, equation in physics: E = mc².

Those who wish to use relativistic mass will want to assert that this statement describes the total energy of the system, using the relativistic mass to show this: for them E = mc² means E = m_relc² = γm₀c².

On the other hand those preferring mass to mean rest mass would say that E = mc² should be replaced by the “correct” or “complete” expression E² = (mc²)² + (pc)² (or in the other notation E² = (m₀ c²)² + (pc)²). Minutephysics, for example has an excellent video making that argument.



But these two equations are mathematically identical, starting with either one and doing some algebra will give us the other form. There is therefore no mathematical preference for one over the other and each has its value in terms of understanding the physics.

E = mc² is valuable because it stresses the identity between mass and energy and therefore the fact that increasing the energy content of something changes how it responds to forces. For example a particle moving at relativistic velocity in a magnetic field has a radius of curvature that depends on its ‘relativistic mass, and it is harder to deflect a moving object because it effectively has a higher mass. (For this reason I, as a compromise, usually use the term ‘effective mass’ rather than ‘relativistic mass’).

Keeping this equivalence in mind is also helpful in understanding that, for example, a hot cup of water has a larger mass than a cold one (though by a tiny amount), and that a proton inside a nucleus has a different rest mass than it does when outside of the nucleus. These are tricky ideas to grasp if we think of mass as a fixed property of an object. And of course writing energy as E = mc² helps us understand the expression for kinetic energy E_K = (γ-1) m₀c² as saying that E_K = energy when moving (γm₀c²) – energy when not moving (m₀c²)… which seems like a pretty reasonable description.

On the other hand E² = (m₀ c²)²+ (pc)² is valuable because it stresses that momentum is not dependent on having rest mass which helps to correct the confusion students experience when they learn that ‘massless’ photons have momentum. It is also really handy to use in situations where there are relativistic collisions. Finally, this representation also can be used to introduce the idea that the energy of an object is the time-component of 4-dimensional momentum.

This 4-momentum, which Wheeler called the momenergy, has momentum in the familiar space directions, and also momentum in the time direction (which is the energy). The spacetime length of the 4-vector is the energy, which we can see comparing our equation to the spacetime interval writing it as giving the rest energy: E₀² = E² – (cp)² just as the spacetime interval is Δs² = (ct)² – x² (the different placement of c being due to the units we use, not a difference in the physics.)


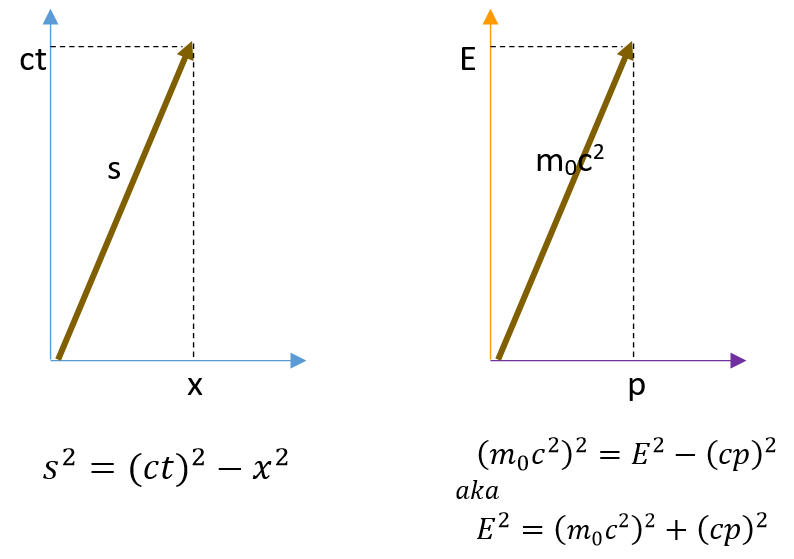Figure 3: Spacetime diagrams for coordinates and for momentum, with Minkowski metric

We are used to different models or approaches being useful in different situations. One would expect we could embrace the idea of multiple models here too, but there is a certain ideological element to the attempted banishment of relativistic mass which sometimes approaches zealotry. It is rather like the banishing of ‘centrifugal force’ from the teaching of physics. Centrifugal force is an illusory force that is seen in a rotating coordinate system. Because it is frame dependent, it can lead to significant confusion for students, and I grew up with the oft-repeated refrain that “there is no such thing as centrifugal force” ringing in my ears. However you will still find plenty of physicists who use the idea routinely, just as they talk about Coriolis forces etc. In the right circumstances the idea is quite useful. Furthermore, there is another illusory force that we haven’t banished in this way at all: gravity! In General Relativity the “force” of gravitation is an illusory force in exactly the same way that centrifugal force is. We keep that concept, though, because it is so useful.

There is real merit in advocating caution in the use of relativistic mass because it does not port very well into realms such as particle physics or even general relativity. But you should not let anyone tell you that relativistic mass is a bad concept. It is just a concept that is useful in some circumstances, and not in others, just like any other physics concept.

Proceed with caution.
If you use rest mass/relativistic mass:
What objections/caveats should one raise about the relativistic mass concept at different levels?

The first is with reference to gravity… where the fact that mass is a property of a system makes things tricky. A rapidly moving object can have a very large ‘relativistic mass’, but it won’t turn into a black hole or anything like that. Light is affected by a gravitational field, but not really as if it had a mass m = E/c². Yet the gravity of two orbiting objects really is different than if they were at rest, and light is affected by and generates gravity. So it is complicated… where gravity is concerned “relativistic mass” is likely to steer us wrong.

Another and more advanced issue with relativistic mass is that it obscures the deeper ideas by transferring the importance from the “geometry” to the “object”. For example consider the argument that “You can’t reach light speed because the closer an object (say a spaceship) gets to light speed the more massive the ship becomes and the harder it is to gain speed.” That’s not exactly wrong… it is a perfectly coherent argument and what it says is true. However, it hides the fact that light speed is not just unobtainable for ‘practical’ reasons – there is something more important there. Light speed is a limit not because it is impossible to get to, but because of the essential structure of the universe, it is the universal maximum speed. This and other things follow from the fact that this speed is an absolute for all observers, and the limit is woven into the nature of causality. Light speed is the limit because it isn’t a speed, just as ‘infinity’ isn’t a number. Infinity isn’t something you can get to by just ‘adding more’ and the speed of light isn’t something you can get to just by ‘going faster’. Light speed is the universal speed, equal to one second per second. For someone observing themselves, this is just the passage of time. However, if you are moving relative to me, your time is mixed with space for me. The faster you go, the more space is mixed in. When you reach the speed of light then your time reaches the point that it can’t be any less and your motion in space is ‘maxed out’. This means that ‘mass increases because you can’t reach light speed’, and not you can’t reach light speed because mass increases.” This is a more basic idea than a merely pragmatic limit, which the idea of increasing mass tends to give to students.

If you want to avoid relativistic mass:
If you make the choice to eschew relativistic mass you will avoid the issues above, but add a few new ones.

One problem is that this way of talking about mass can cause some people to think of mass as somehow separate from energy… you hear people saying things like “mass is converted to energy”, which as someone once pointed out is like saying “my car was converted into an automobile”. In this respect there are arguments both for and against relativistic mass. Using the idea of relativistic mass stresses the connection between mass and energy concepts, since we treat energy as mass in this way. On the other hand we could argue against relativistic mass by pointing out that since ‘relativistic mass’ and energy are the same thing why have two words? Use ‘mass’ for the thing we use it for in our everyday experience (the “rest mass”) and just use ‘energy’ for the other. This does make some sense, but not always. It’s complicated.

If you want to eliminate the idea of relativistic mass then you should also make clear that mass (formerly known as rest mass) is the property of systems, not objects. The mass of a system is not, in general, equal to the sum of its parts. Further the mass is no longer related to force and acceleration — that link is already broken in special relativity, but the break is more complete if we define mass this way.

A General Suggestion:
Physics is, and should be, a multicultural place just as Canada aspires to be a multicultural country, and I think the same precepts apply. Whether you view the idea of relativistic mass as useful or harmful it is perhaps best to recognise that cultural diversity can enrich our understanding and we don’t have to have everyone conform to one point of view to work together. And maybe if we teach our students that these different perspectives exist they can learn that lesson too. Peace, order, and good physics!

Tags: Modern Physics