Chris Meyer, OAPT Past President, TDSB hybrid teacher-coach
Christopher.meyer@tdsb.on.ca

Back in the day, I used to teach at the Ontario Science Centre and present their school programs. I would meet the visiting teacher and mob of grade 9 students in advance of my “Cosmic Connections” program and ask, “So has your class covered the astronomy unit yet?” On more than one occasion, the teacher answered, “No. You’re it!” That’s right; my 45-minute extravaganza was all the astronomy that students would get in grade 9. Despite fifteen years passing since then, the topic of astronomy still does not fall within every teacher’s comfort zone, so I hope that sharing the resources for our inquiry-based unit on grade 9 astronomy will help. In this article I will explain the ideas and pedagogical design of our unit and hopefully encourage you to check it out!

Big questions, big ideas, big things
Astronomy is a great topic for tackling big questions. There are many to choose from and I have chosen to begin the unit with two: why do the Sun and Moon move across the sky the way they do and how does the Sun work? As we explore deeper, astronomy becomes a study of origins: where do stars, planets and galaxies come from; and where do the elements of the periodic table come from? Astronomy is a story told mostly by light, so the colours and speed of light become powerful explanatory ideas. Math has a prominent role in this unit, serving as an important tool for making sense of the vast quantities involved in the contemplation of space.

Astronomy is familiar
The study of astronomy can feel abstract and distant, so I think it is important to focus on the most familiar celestial objects: the Sun and Moon. Students can see these objects almost every day, unlike even the stars (for us city-folk). For this reason I hardly mention constellations. And, students spend so much time indoors, basking in the glow of their electronic devices, that they rarely see the sky at night. So, I focus on daytime observations. I want my students to be able to look up each day (away from their devices) and understand what they see: why the Sun is so low right now (January) even at noon, why it rises at different positions along the horizon, why we see the Moon both day and night, why eclipses don’t happen every month. These are things we often notice, but don’t think about. To make sense of all this, we need to visualize what is happening.

Visualizing movement in the heavens
The motions of the Sun and Moon are both simple and intriguingly complex – their nuances have kept astronomers busy for many hundreds of years! We focus on three important rotations: the Earth’s orbit around the Sun, the Moon’s orbit around the Earth, and the Earth’s rotation around its axis. Students need to connect this new scientific terminology with their everyday knowledge of these cycles.

Fun Question: Which rotation takes (roughly) one day, one month, and one year?

Diagrams are a powerful tool for representing and understanding what we see in the sky. We start by introducing polar diagrams of the sky and sun path diagrams, showing the position of the Sun in the sky at different moments during one day. Here are PowerPoint slides from the Astronomy Course Guide showing these diagrams:



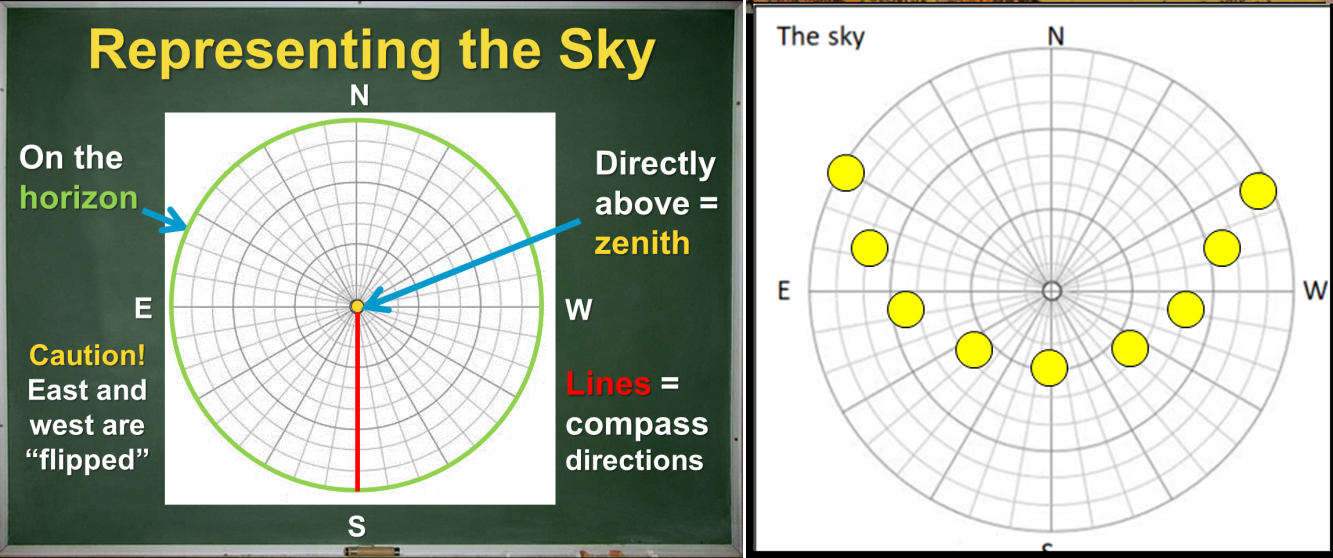
Fun Question: In Ontario, do we ever observe the Sun at the zenith?
Fun Question: In Ontario, which season does the sun path diagram above represent?

We can also create a polar diagram for the Moon and track its “movement” across the sky too!

Fun Question: Which rotation is responsible for the Moon’s apparent motion across the sky? How much time does it take for the Moon to cross the sky?

Another tool we use is the Sun-Earth-Moon System diagram. This shifts the point of view from the Earth (like in the sun path diagrams) to the “fixed stars” looking down on the solar system and Earth’s north pole. It allows us to visualize the Earth and Moon at different times and predict what Moon phase would be visible. The dot on Earth represents an observer.



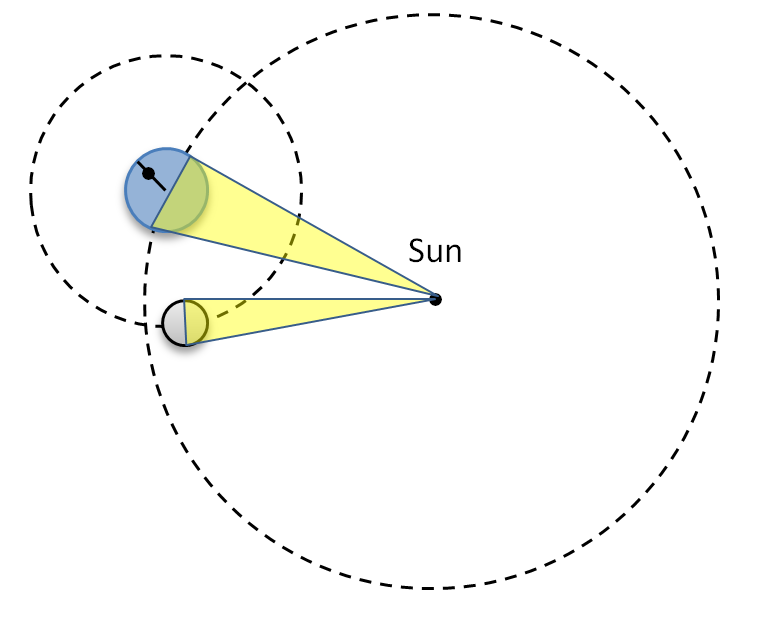
Fun Question: Most diagrams of the solar system are horribly out of proportion. In what ways does this diagram have the wrong proportions?
Fun Question: According to this diagram, roughly what time of day is it for the observer? Is it closer to sunrise or sunset?
Fun Question: In a few hours, roughly what phase of the moon would the observer see?

Students need to understand that most of the drawings we make of the sky and solar system are not in correct proportions: if the distances between objects are, the diameters are usually not; and vice versa. If both are, you probably have a diagram or representation that does not fit on any page. Despite this challenge, understanding the correct proportions is an important part of making sense of space!

How big is it? Using math in grade 9 astronomy
The purpose for asking a question like this is to make sense of something, like the enormous size of the Sun compared with Earth. However, punching numbers into a calculator and hitting “equals” does not accomplish this. Both the mathematical process and its result have to be mentally processed before it can make sense to our students (and perhaps our teachers too!). All of this requires a lot of explicit structure: lots of scaffolding for their math work and sense-making processes. The structure is important for two reasons: the very wide range of math abilities in our science classroom; and the different habits and practices of math work in science compared with a math class.

Numbers in astronomy
Let’s start with scientific notation, which people actually use to make their lives easier! This is, quite frankly, hard for students to believe so it’s our job to help them.



Fun Question: Try it! How long did it take you (without using the planet names, of course!)?

Scientific notation allows for very quick comparisons of size and reduces the “you missed a zero” error. Students will need explicit guidance on how to use their calculators:



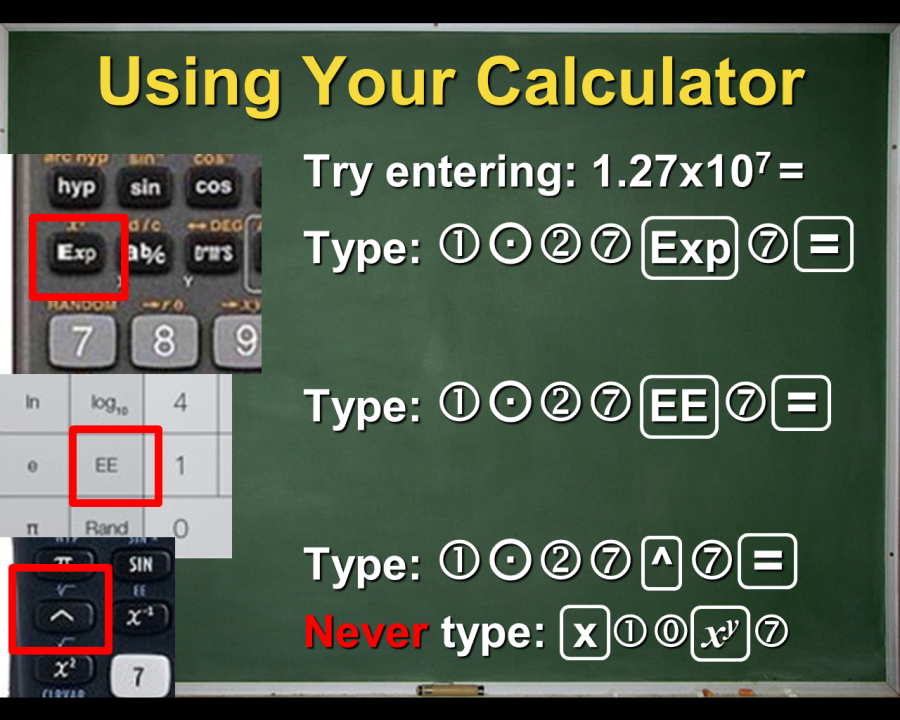
A common student mistake is typing in: 1.27 x 10 x^y 7, which bungles the order of operations when dividing by this number: watch out for this! And here’s another number challenge: the age of the universe is 13.8 billion years, what is this number written in scientific notation? We need to help students practice transcribing between number words, standard decimal notation, and scientific notation.

13.8 billion years ↔ 13.8 x 10⁹ years ↔1.38 x 10¹⁰ years ↔ 13 800 000 000 years

Did you notice I kept writing “years” with each example above? Numbers in science usually represent measurements and do not make sense when written without units, so train students to write a unit with every measurement number. To help students practice their number writing skills, we use a summary page for the exotic numbers we encounter in this unit.



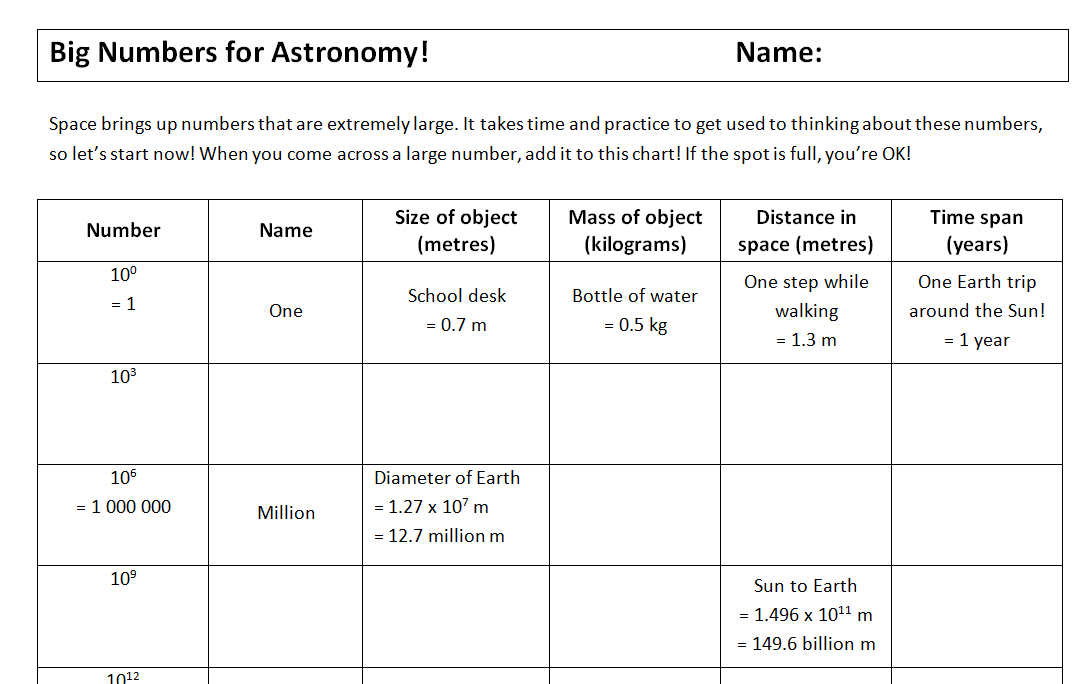
Conversions in astronomy
Things get big, really big out there in space: a single star can span the radius of Jupiter’s orbit (bonus points if you can name such a star!). The convenient units of measure for our humble lives here on Earth produce enormous, inconvenient numbers when measuring astronomical objects. So, we need to convert between units. Students usually accomplish this by taking the original measurement and randomly multiplying or dividing it by the “conversion factor”. Whether the result makes sense is unimportant to them. Here is where structure and sense-making habits need to kick in. Everything we do mathematically should be carefully organized. Here is a sample conversion from the lesson:



An important part of understanding the mathematical conversion process is showing that the original units divide away. This is what convinces us that we have set up the math work correctly. But to make sense of the result, students need to be prompted to reflect, and question #3 in the above example does exactly that. This is based on an important concept: converting to a smaller physical unit yields a larger number (more of those units).



This is how we make sense of the conversion process: by understanding how the number part should change.

Fun Question: How should the number part change when converting from:
a) Meters to centimeters?
b) Hours to years?
c) Light years to astronomical units? Whoa, getting ahead of ourselves!

Calculations in astronomy: proportions
An important kind of question we ask in astronomy goes like this: if the Sun is this size, what would be the size of Earth? This allows us to construct scale diagrams or models and get an appreciation for how sizes compare. Much like our conversions, these calculations need to make sense. But unlike a density calculation, for example, there is no prefabricated equation to plug the numbers into. Students need to construct mathematical expressions for each calculation and this is a hard process. Understanding is needed, so we go back to the concept of the ratio:



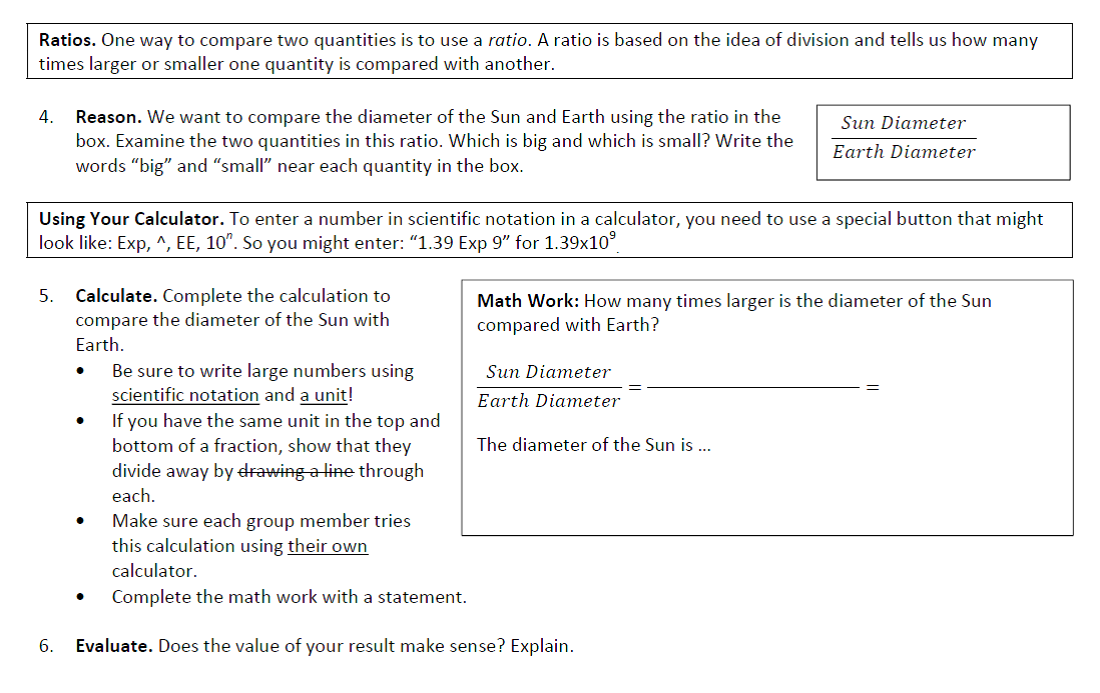
Notice all the structure that guides students’ mathematical work and sense-making. They will not do this unless you insist on it every time! In this example, students are trying to choose an object to best represent Earth in correct proportions to a ball that represents the Sun. We continue the math work by thinking about how to use this ratio result and making sense of the mathematical challenge: should we multiply or divide with it? The full calculation process is carefully modeled (written out explicitly) and explanatory notes are given for each step. These notes will become the reminders students use when they complete a full calculation on their own.



I find this level of structure is helpful for both the weak students and the strong ones (an example of universal design for learning). Many students who are comfortable with the math work don’t actually understand it or are terrible at thoughtfully explaining it. This structure forces them to think about what they are doing and describe it clearly. Since it is modeled so carefully, I don’t accept (i.e. award marks to) any work that has any significant errors or omissions.

Calculations in astronomy: speed, distance, and time
The most important speed in the universe is (no, not your internet speed) the speed of light. The amount of time light takes to travel from place to place affects how we interpret what we see in the sky and the signals we receive from the sky. Light’s travel time is important for “short” distances within our solar system and is crucial for great distances across our universe. It helps explain why looking deep into space is the same as looking back in time. And like our previous work with math, our speed, distance, and time calculations are highly scaffolded with prompts for sense-making.



The importance of math outside the math classroom
Phew, that’s a lot of discussion about math! But the discussion is worthwhile because treating math carefully outside the math classroom is important. One reason is that there are different conventions or habits for math work in math class and in science – we focus on different things, so we go about doing and writing math in different ways. It is easy to forget or overlook this, which causes confusion for our students. The second reason for our careful approach is how science uses math: as a tool that is chosen to help us understand something about our universe. As a result, we strongly emphasize the sense-making steps involved with math work and math’s explanatory power. This emphasis can help students better appreciate the value of mathematics. The high level of structure and purposefulness of this approach can help them overcome some of their reluctance to do math and provide another opportunity to make sense of the mathematical techniques they (hopefully) regularly use. An example of the latter is students’ habit of “cancelling out” quantities in a ratio. This becomes such a routine that many students forget what mathematical operation is actually taking place (division) and that when terms divide out the result is one and not zero (students say the quantity “disappears”, which to them corresponds to the idea of zero).

Fun Answers

• Earth’s axial rotation, the Moon’s orbital rotation, and Earth’s orbital rotation
• Nope! We live further north beyond the tropic of cancer.
• Summer – a long sun path = many daylight hours, sunrise and sunset occur to the north
• Earth’s rotation about its axis, one day!
• Many! The diameters of the object are out of proportion (Sun too small, Moon too big) and the distances are off (Earth too close to Sun, Moon to close to Earth)
• It is a bit before midnight, closer to sunset.
• Roughly half, maybe a bit more shaded than lit.
• How long did it take you? Did you find the first one sufficiently annoying?
• The number part gets bigger, smaller, bigger.
  

What’s next?
In part II we will look at light and chemistry!

Tags: Astronomy, Pedagogy