Chris Meyer
President, Ontario Association of Physics Teachers
Hybrid Teacher-Coach for Science, Toronto District School Board
christopher.meyer@tdsb.on.ca

I have a question for you to think about, which I have chosen for two reasons: first, it is about electric circuits, which are fun; second, answering this question well requires thinking carefully about how we describe circuits. If you work through it carefully, you should discover one important reason why many students and teachers get tripped up when thinking about electric circuits. Now, I don’t want you getting bogged down in the weeds on this, so let’s start by assuming the devices are ohmic, meaning they faithfully obeys Ohm’s law. My question is this:

Which bulb would be brighter: a 10 Ω bulb or a 20 Ω bulb?

Take a few minutes to think about this question. What assumptions are you making about the circuit in which this bulb is found? Can you think of an example where either answer is the correct one?

Did you pick the 10 Ω bulb to be the brightest? If you did, you’re right! Well, from a certain point of view…

A little bit of reasoning tells us that if we increase the resistance of a load, the current will decrease while the voltage drop remains the same. This is Ohm’s law in action. Couldn’t be simpler, right? The simulation below illustrates this nicely.



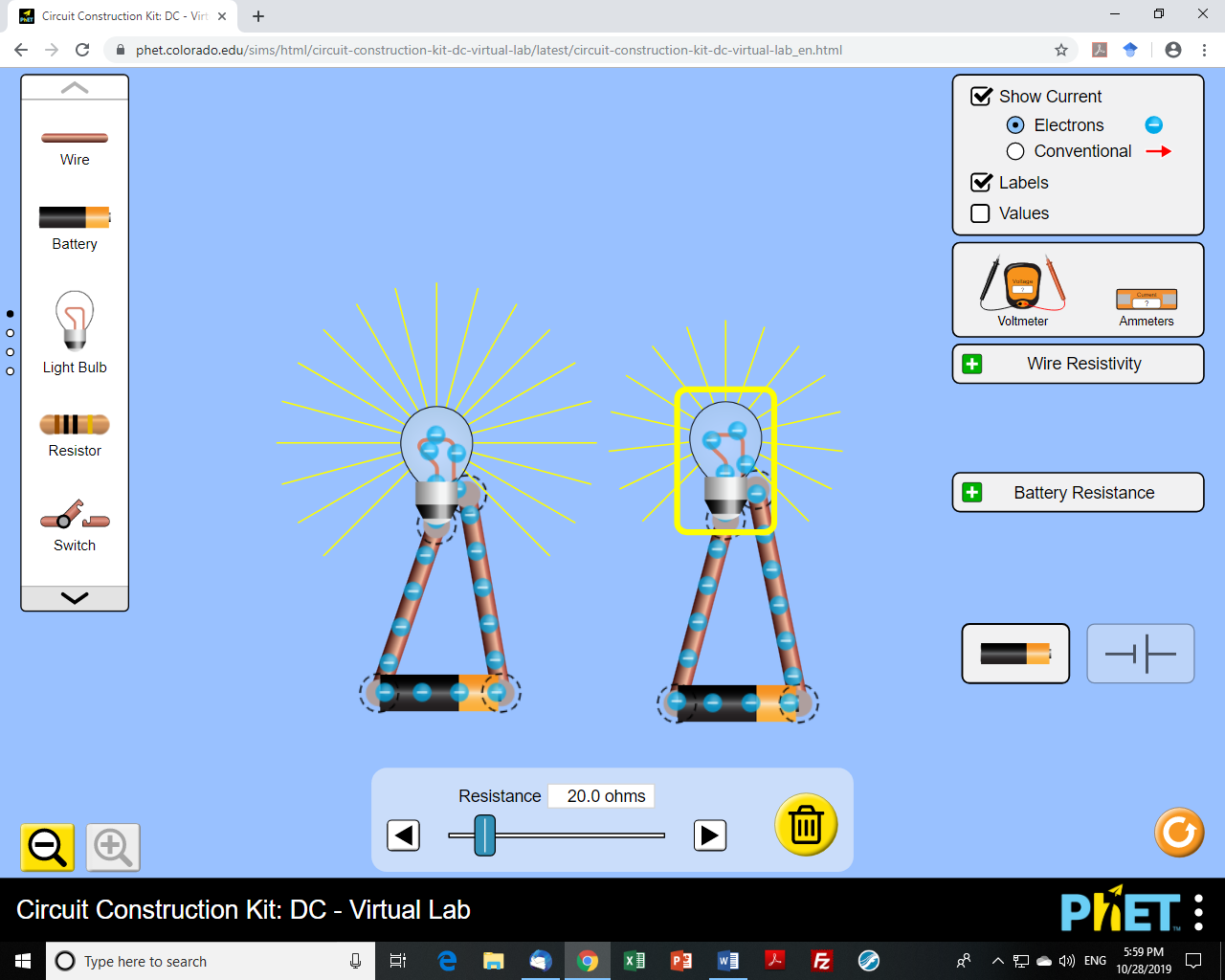
But did you pick the 20 Ω bulb? If you did, you’re right!

The idea of resistance is related to the obstacles electrons encounter as they pass through a load. The more obstacles, the greater the energy loss and resistance. And where is that energy going? To heat and light, of course! So, the bulb with the greater resistance will transfer more energy from the system of electrons to the bulb and produce more light! The simulation below illustrates this nicely.



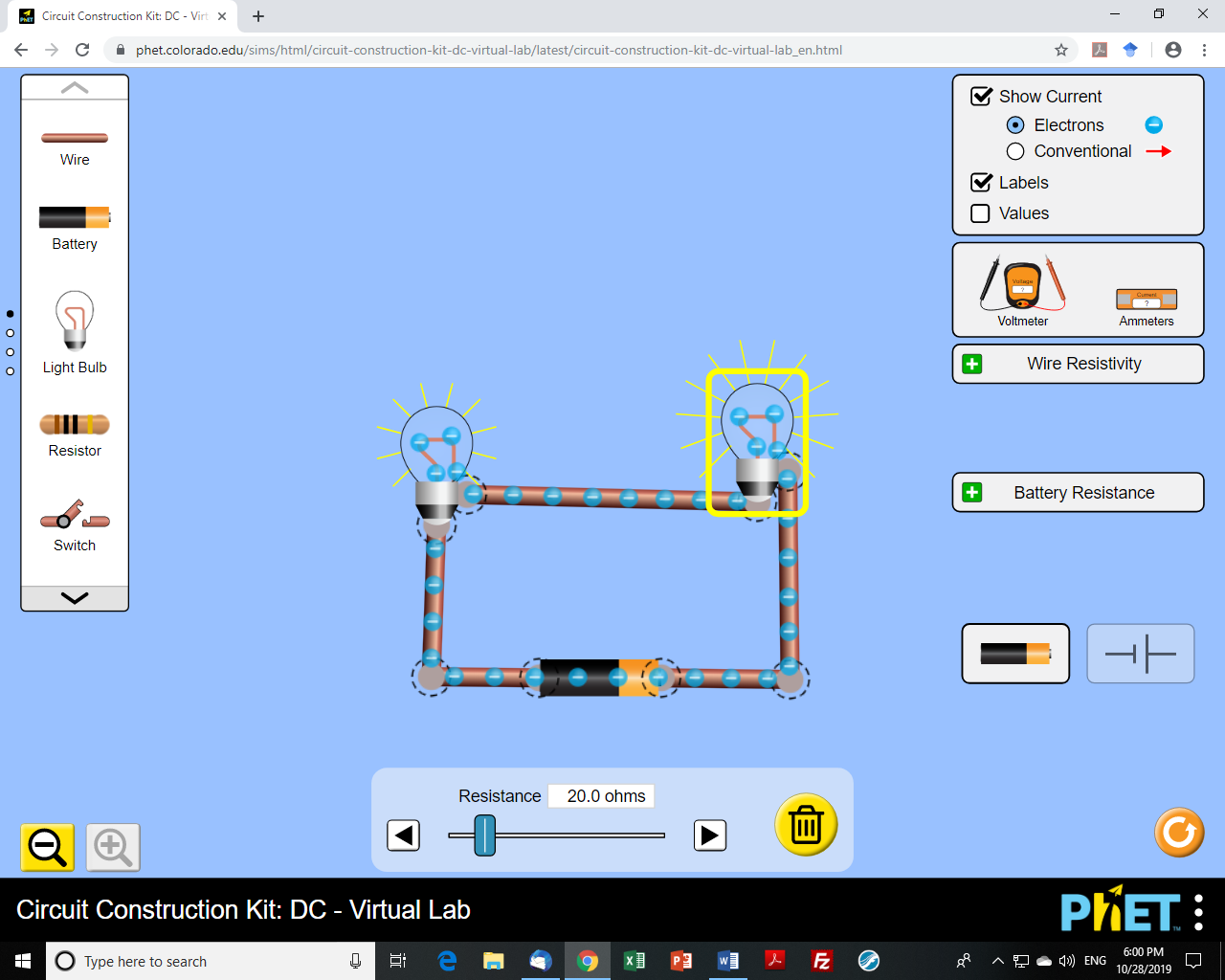
I chose this question because I was stumped by it when it was posed to me by a teacher. And then stumped again when it was asked a year later by a student. Each time, we were stuck because we did not have a clear circuit in mind, or we were not clear on what we were comparing and discussion made things worse. This mental shortcoming has caused me and my students much grief over my 21 years of teaching. Until last week.

Handy trick: define what you are comparing
Sometimes the question seems so clear cut: “Does the resistance affect the current?” That might be all the student says, so you confidently reply, “of course it does: increase the resistance and the current drops.” But you had in mind a single bulb circuit with low resistance compared with another single bulb circuit with high resistance and the same source. However, the student was thinking about two bulbs in series, where one has a larger resistance. The result of the conversation is that you have confirmed the student’s strong suspicion that the current in fact drops in a series circuit after going through the larger bulb (it doesn’t). Yay, education! This can even happen when you and the student are staring at the same drawing of a circuit. Unless we explicitly (meaning out loud) define our comparisons, we can easily switch back and forth in our minds between the types of comparisons we are making. I define two types of circuit comparisons:

• A Same-Circuit Comparison: here we are comparing measurements taken within the same circuit.
• A Different-Circuit Comparison: here we are comparing measurements each from different circuits.
  

This almost seems trivial, but I would bet these confusions are the cause of almost half of my students’ flawed thinking about circuits and half of the miscommunications between me and my students. (The other half is likely confusion about the meaning of voltage measurements – a topic for another day.)

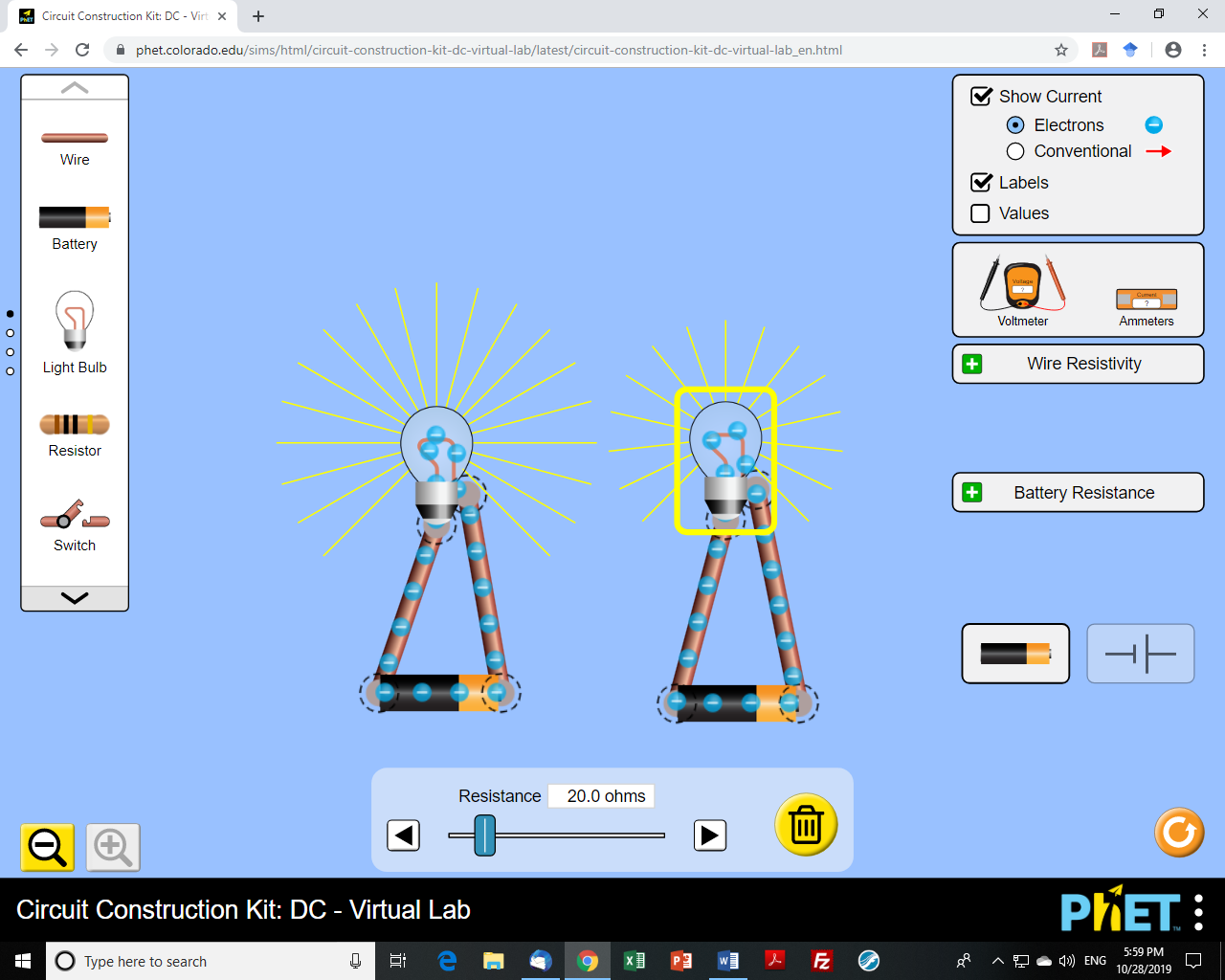
Here is the circuit I was discussing with a student last week when I was asked, “Doesn’t the resistance affect the current?”



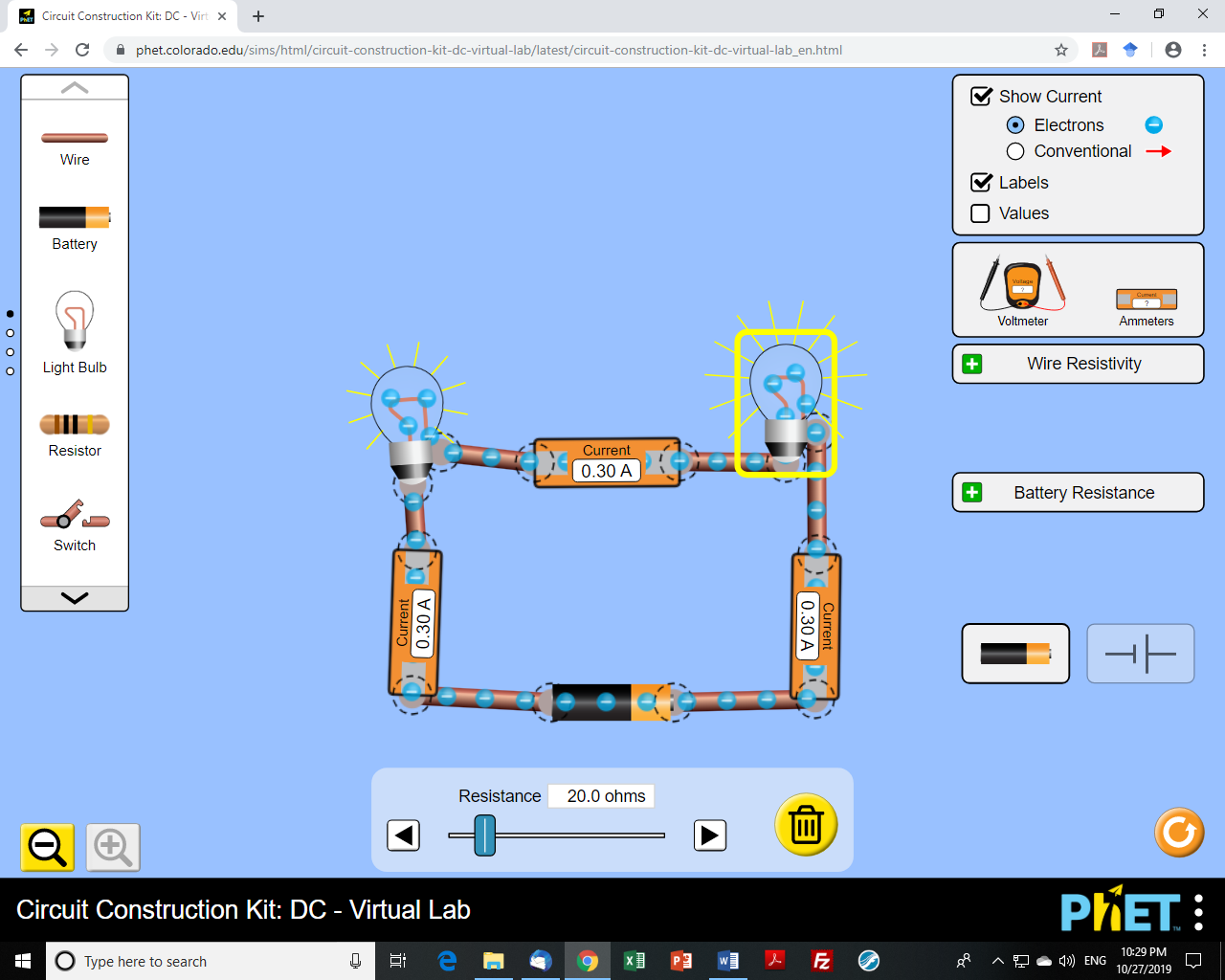
The student felt there was a problem here because there was one bulb with a larger resistance, yet the current was the same! The student was thinking about Ohm’s law and a different circuit comparison, where an increase in resistance should cause the current to drop. However, I didn’t clue in to this yet; instead, I confirmed that, “the current should be the same everywhere in the circuit”, making a same-circuit comparison and mentally noting that the resistance doesn’t even matter since it’s a series circuit! Now as far as the student was concerned, I might as well have been saying that Ohm’s law simply doesn’t work here. Seeing a puzzled look on the student’s face, I tried again. “Let’s compare this carefully. Look at these two different circuits. We can increase the resistance of a bulb in the second circuit and the current will decrease.” The second circuit is this one here:



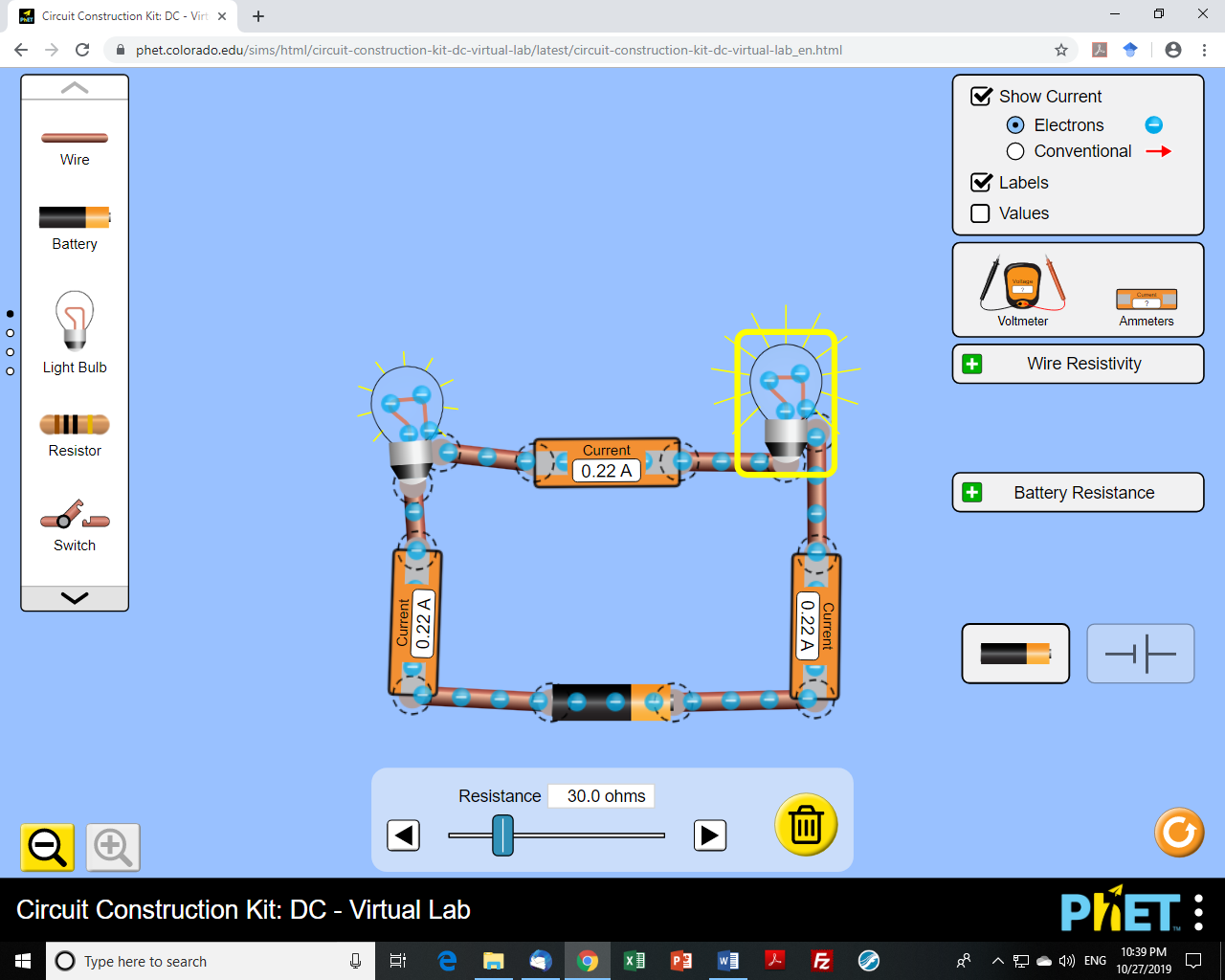
“Yes, increasing the resistance of a circuit element will decrease the current through it. We see that when we compare these two bulbs from the two different circuits. But look at the current measurements in the second circuit. These measurements are all from the same circuit. How do these measurements compare? They are all the same since it’s a series circuit. How does a current measurement here compare with one from the other circuit? It is lower because of the increased resistance the battery experiences.”

These types of situations come up all the time. Another way I try to make the comparisons clear is by referring to the simple, one-bulb circuit as our reference circuit.



This provides a convenient label so we’re not always saying “that circuit from yesterday’s class” or “the first circuit we made”.

Challenge yourself to make your comparisons explicit and ask your students to do the same. It’s not pedantic, it is the level of detail that is necessary to clearly express our physical understanding of these “simple” situations.

Tags: Electricity