October 02, 2016 Filed in:
ArticlesJohn Berrigan, Teacher Oakville Trafalger H.S.
berriganj@hdsb.ca
In the
previous article we learnt how to find the largest possible delta-V that a rocket can experience. In this article, we are going to find the thrust of a rocket by using the fundamentals of conservation of momentum. This will be similar to what we did in the last article, however this time we will use variables instead specific masses and velocities. Furthermore, the cart is now a rocket, as this is rocket science!
Suppose we have a rocket of mass
M, moving at velocity
V. During a time interval of
Δt, it will eject fuel with a mass of
Δm at a velocity of
Vexh relative to the rocket (exhaust velocity). As usual, momentum is conserved and the momentum before is equal to the momentum after.

The momentum afterwards, consists of two parts. Going one way is the reduced rocket mass travelling at the increased velocity. Going the other way is the fuel, whose velocity is a combination of the exhaust velocity and the rocket’s velocity. Using conservation of momentum, we have:
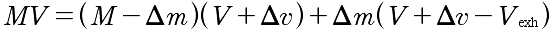
Once expanded we have:
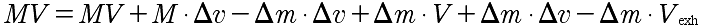
After lots of cancelling, this simplifies to:
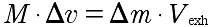
Divide both sides by Δt to get:
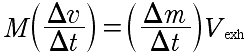
where
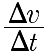
is acceleration.
So the left side is just
Ma and therefore the net force acting on the rocket, which in this case is the thrust of the rocket.
Therefore,
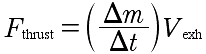
.
Does this formula make qualitative sense? It says that to increase thrust you either need to increase exhaust velocity (how fast you throw the fuel out the back) or increase the rate at which you use up your fuel. Play around with the simulation below and convince yourself that these factors affect the thrust and total delta-V.
Before running the simulation, predict the following. For a given amount of fuel, does changing the fuel use rate affect the total delta-V that the rocket experiences?
http://www.jabe.com/Space/thrust.htmlAs a last point, the formula
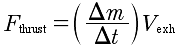
can be written in the impulse form,
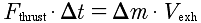
. In 12U physics we usually deal with impulse in the form

. Why are they so different?
These two equations are just specific cases of the more general impulse equation
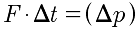
. Since
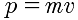
,
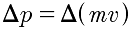
and through the chain rule,
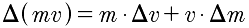
. In most of the 12U problems, the mass doesn’t change, so the second term is zero. However, the mass definitely changes for rockets but the exhaust velocity can be kept constant. (Note: The derivation using the chain rule is only valid if
Δm << M. See
this Wikipedia article for a brief discussion.)
We now have two ways to increase the thrust of a rocket. Increase the rate at which we use the fuel or increase the exhaust velocity. For a given amount of fuel it would seem best to throw the fuel out as fast as possible.
Next up in this series of rocket articles, we will explore how the efficiency of rocket engines can be defined. Soon we can head to Mars… but not quite yet. Ad Astra.
Edited November 3 to fix minor typographic errors.Tags: Forces, Kinematics, Momentum, Motion



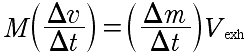 where
where 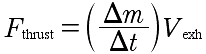 .
.