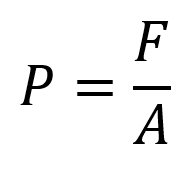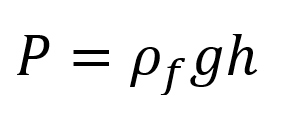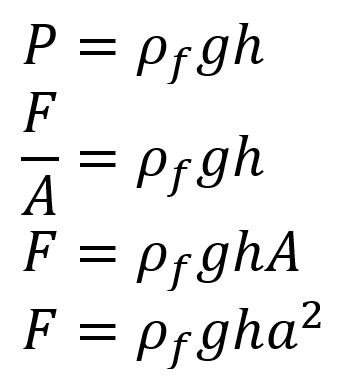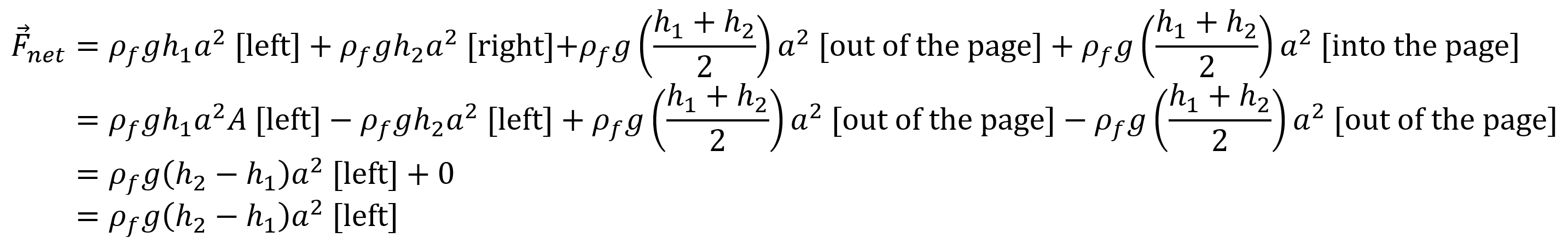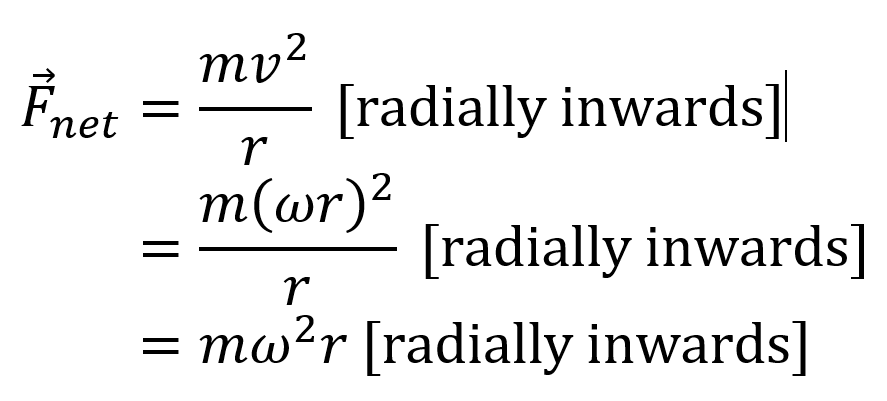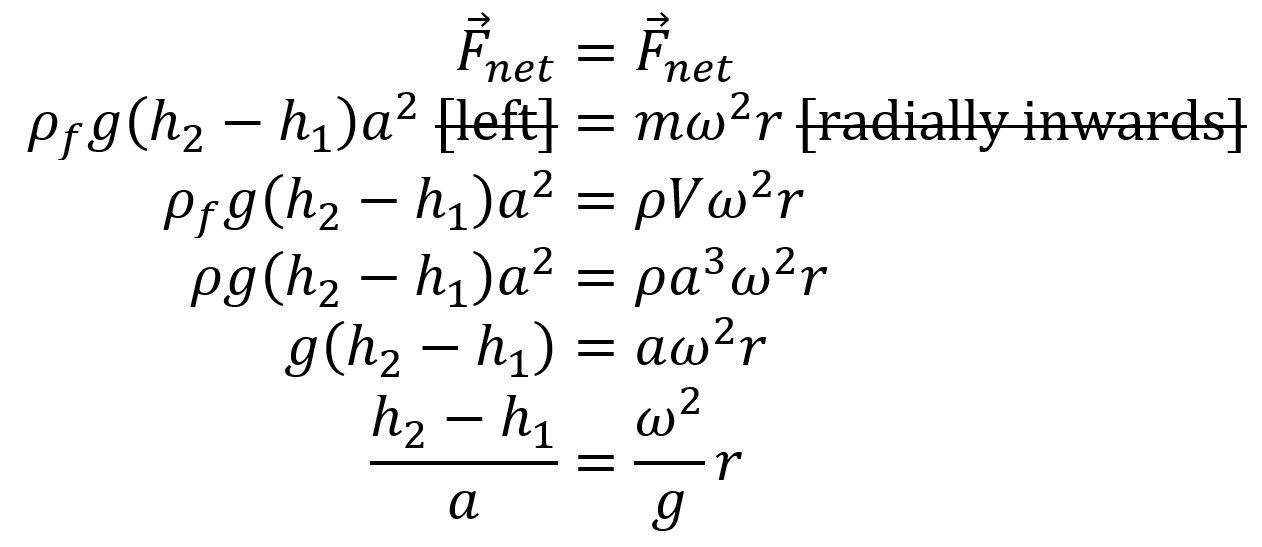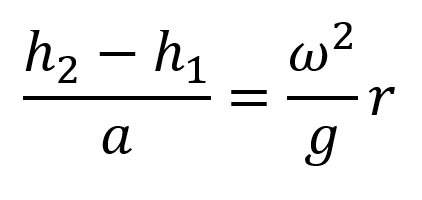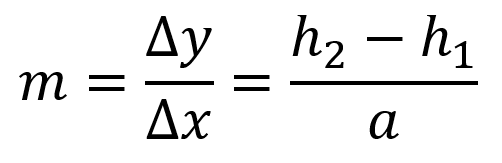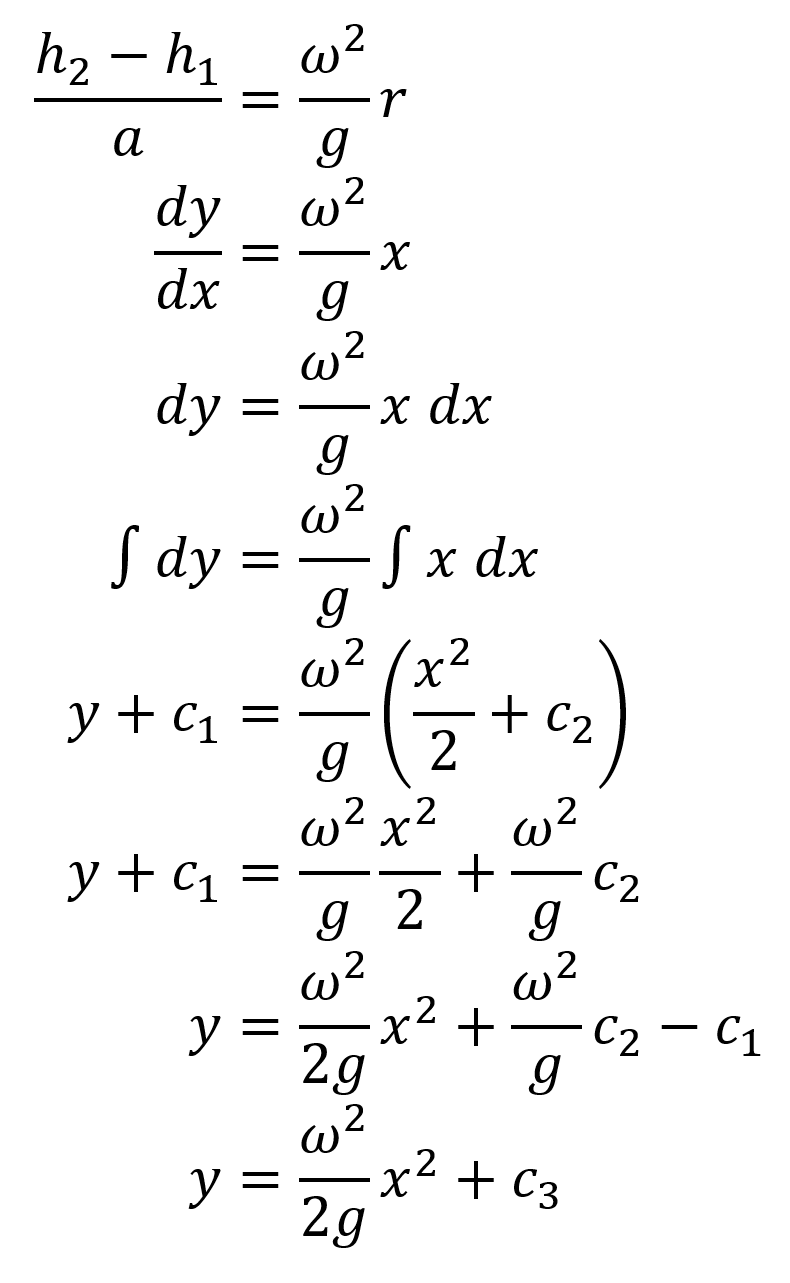Eric Haller, Occasional Secondary School Teacher, Peel District School Board
rickyhaller@hotmail.com

In science, it’s always nice to be able to do a hands-on experiment. While there are many experiments you can do in class, there are some you can’t. Sometimes a particular experiment may require expensive equipment that you don’t have, may take too long to set up, may yield data that is too imprecise to analyze properly, or an experiment may be too dangerous for a classroom setting. At the latest annual OAPT conference Andrew Moffat showed us several websites with video libraries filled with experiments that I wouldn’t be able to recreate myself (skip to the end of this article for those links). To give you a taste of what kinds of videos are available, and how you might build a lesson around one of them for your students, I’d like to analyze one of my favourite videos from the collections.

Question: If you filled a fish tank halfway with water and placed it atop a Lazy Susan or turntable and spun it around, what shape would the surface of the water form?

Stop reading and take a minute to think about.

Now that you’ve thought about it, keep that shape in mind and watch the video below.

Figure 1: A video showing what happens when a fish tank is spun around.

From the video you might notice that the surface of the water looks parabolic (in three dimensions we could call this a paraboloid). We can actually derive whether or not it is parabolic in shape using grade 12 physics. I’ve made a worksheet for the students to follow along with here, and you can access the solutions here if you want.

The following is an in-depth analysis of this phenomenon that you could use to explain this experiment to your students.

When something is submerged in a liquid, it feels pressure pushing in on it. Pressure is equal to the amount of force pushing on an object, per surface area. Mathematically,

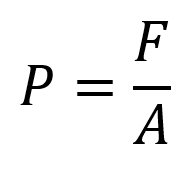
Here, F is the amount of force pushing on the object, A is the surface area of the object, and P is the pressure applied on the object, measured in newtons per square metre. If you’ve ever dove down to the bottom of a swimming pool, you’ve probably noticed a higher pressure, and water may have gone in your ears when you did. The more water that is above you, the more weight of it you feel crushing down on you. Water-pressure increases linearly with depth, the relationship being

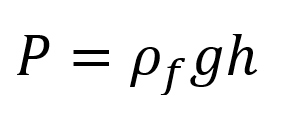
Here ρ_f is the density of the displaced fluid (not the density of the object displacing the fluid), g is the acceleration due to gravity, and h is the depth of the object in the water.

In order to find what shape the surface of the water makes, let’s not talk about the water itself, but instead focus on a single fish floating in the rotating fish tank. As is tradition in physics, let’s oversimplify the situation and assume the fish is shaped like a cube; henceforth, we’ll call it a cubefish. Also, so that the fish behaves like the water would, assume the cubefish has the same density as the water around it, which is actually a good approximation because fish often float in place.


Figure 2: My artistic rendition of a cubefish.

Note that for our submerged cubefish the pressure pushing up on the bottom of the fish is greater than the pressure pushing down on the top of the fish because the bottom of the fish is deeper, and water pressure increases with depth. The cubefish would of course rise upwards because of this, if not for the fact that gravity is of course pulling it down. The force from the water pressure pushing up on the bottom of the cubefish, the slightly smaller force from the water pressure pushing down on the top of the cubefish, and the downwards force of gravity, must all sum to zero for the cubefish to float in vertical equilibrium. What we’re really interested in though is the pressure pushing in on the sides of the cubefish. Since the top of the water isn’t flat, the depth of the cubefish changes based on which side of the fish you’re considering. The leftward and rightward inward forces won’t balance each other out. Let’s say the left side of the fish is at a depth of h₂ and the right side is at a depth of h₁.


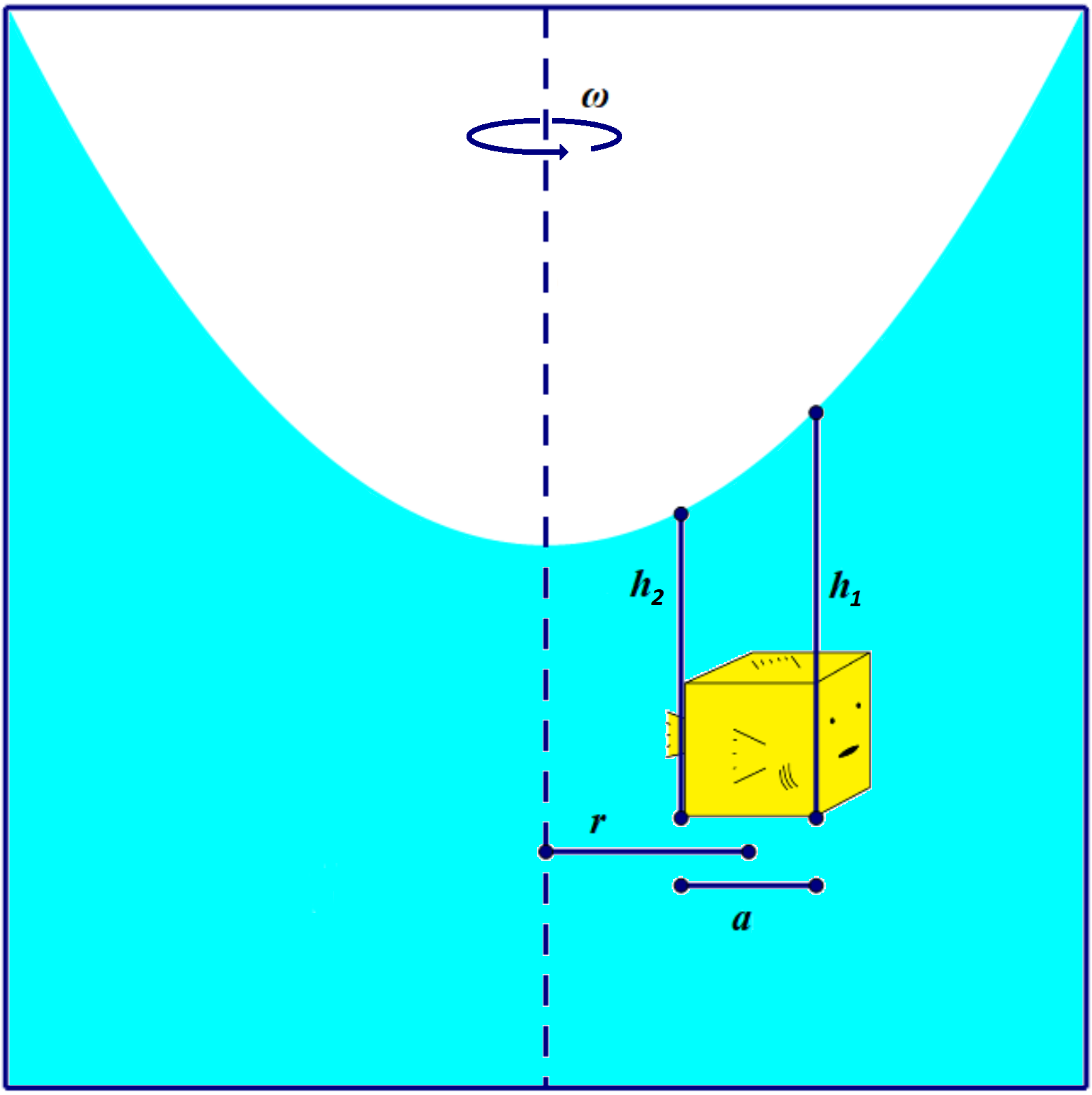Figure 3: The coordinate system we’ll use for a cubefish inside a rotating fish tank.

Combining the equations P = ρ_fgh and P = F/A, and assuming the cubefish has a side length of a, we find:

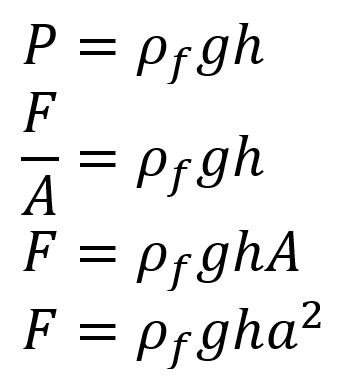
The horizontal net force of the water pushing in on the cubefish is as follows:

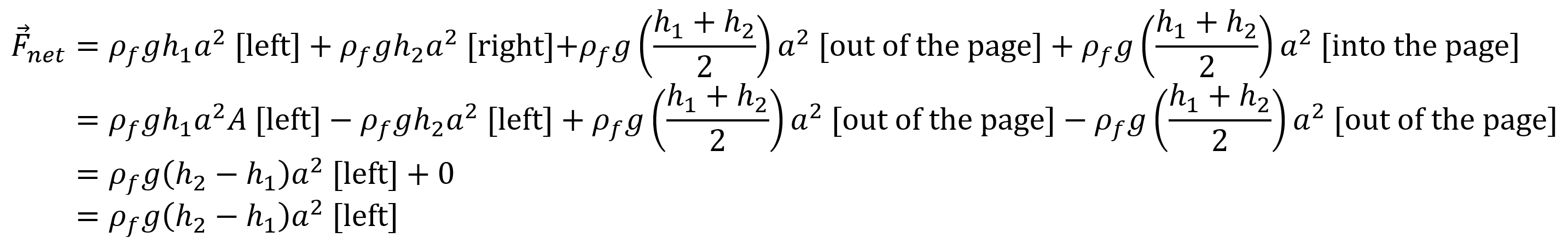
The amount of force required to keep the cubefish going around in a circle at a constant speed, v, and constant radius, r is given by the centripetal force, which, in terms of angular speed, can be written as follows:

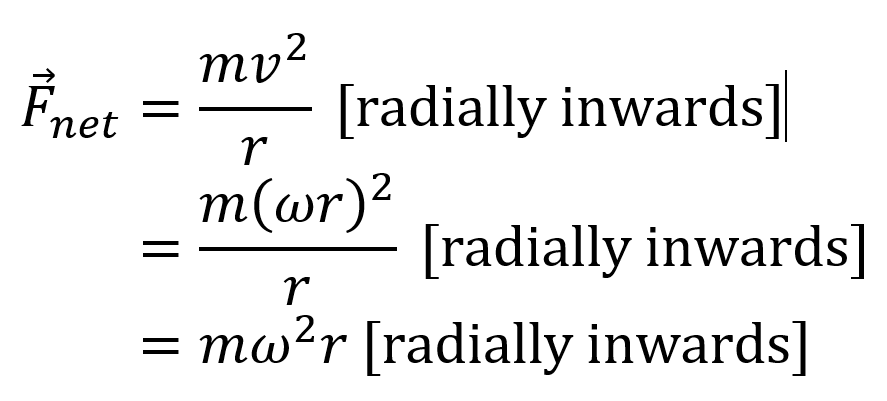
Setting these net forces equal to each other, and using the fact that ρ = m/V, we get:

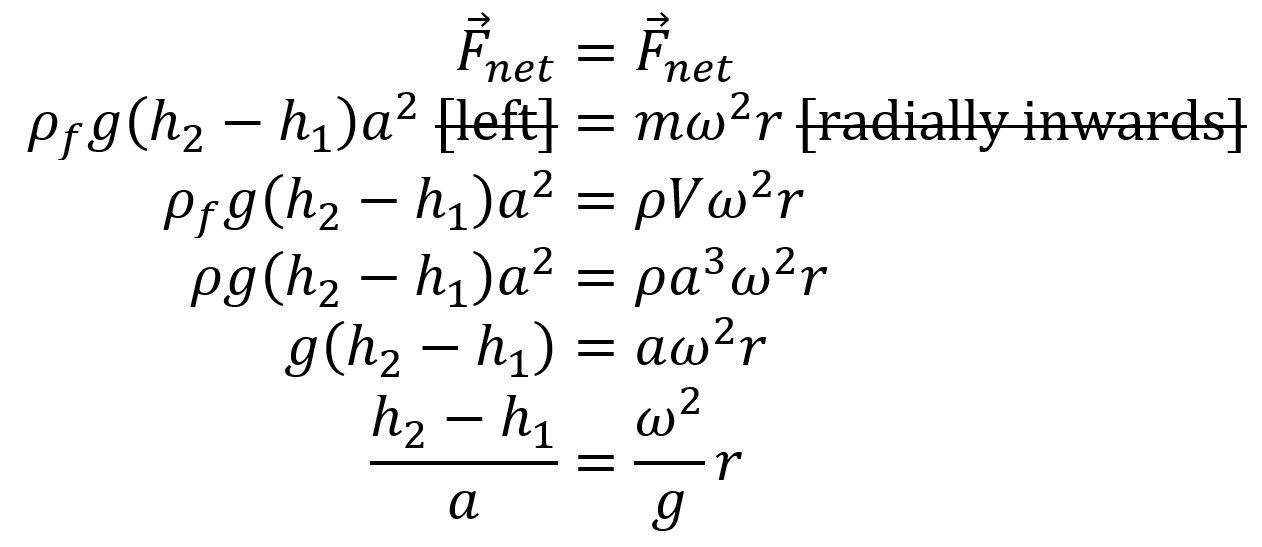
Now let’s consider what that last equation tells us.

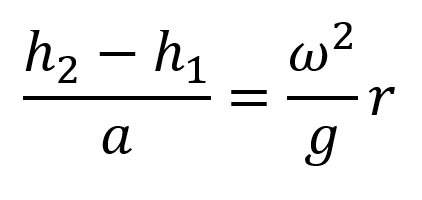
Notice that the left-hand side is equivalent to the slope of the cubefish

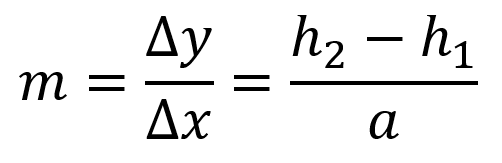
This is literally the slope you would expect to find any cubefish in the tank to float at, meaning that if you had a bunch of fish in the tank, they would not remain horizontally, but would typically conform to some angle, depending on where they were in the tank. On the right side of the equation you can see a dependence on ω₂. This tells us that the faster the tank is spun, the steeper the fish, and similarly, the water level at the surface will be. There is also a dependence on r, this means that the further you are from the centre, the steeper the fish and the water level will be. The dependence on g doesn’t really impact the experiment for us, however if you repeated this experiment on the Moon, the slope of the fish and the water would be greater than it would be at the same angular velocity on Earth.

That equation tells us the slope of the cubefish is proportional to its radius. From calculus we know the only functions that have linear derivatives are parabolas! Hence the proof is complete and the water at the surface will form a parabola. I assume most of the people reading this article have some background in physics and solving integrals, so I’ll derive the exact equation of the parabola for you here, however this is now above and beyond what I would actually show my students.

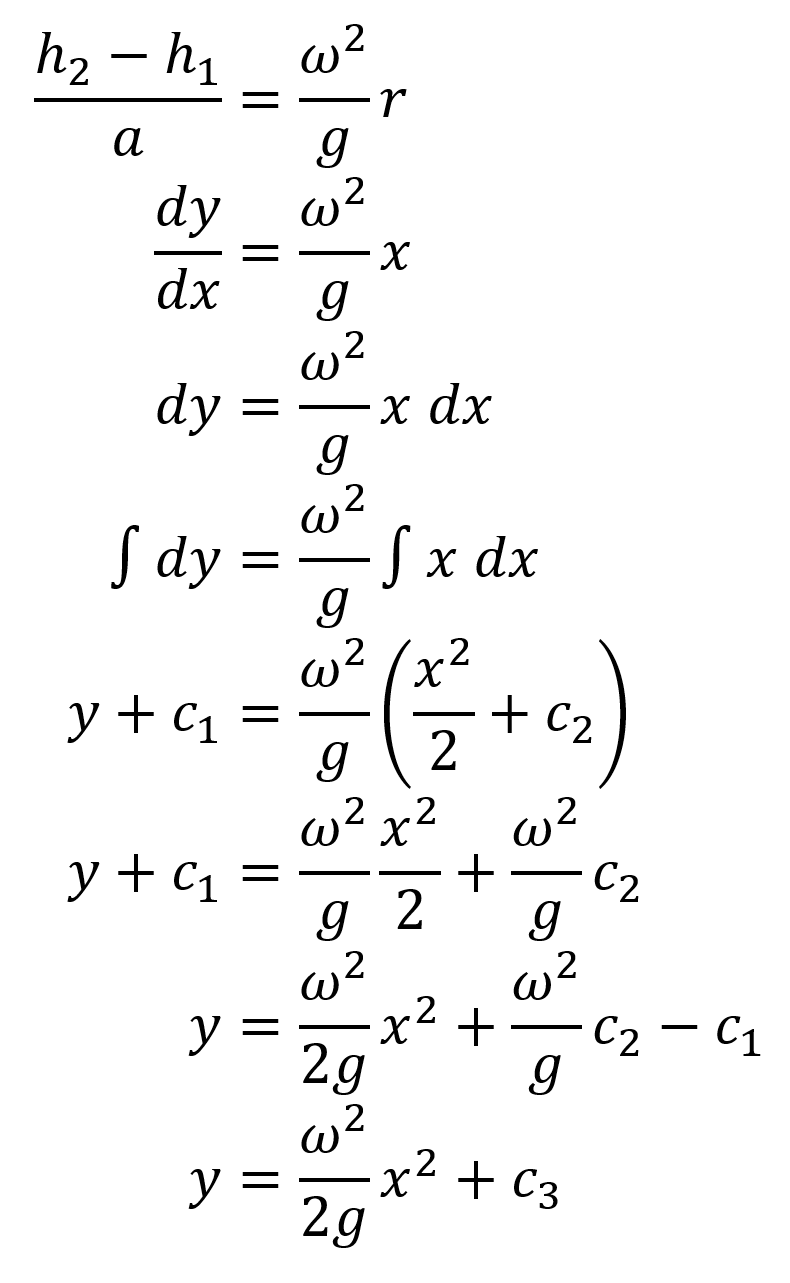
Hence the water on the top of the curve forms a parabola that has been vertically stretched by a factor of ω₂/2g, and has been vertically shifted upwards by some amount, c₃. The rest of the water below the surface follows a family of ‘parallel’ parabolas, just with smaller vertical shifts the further down you go. The vertical shift of the surface of the water can be below the tank itself, when spun fast enough there will literally be no water in the middle, as seen in this GIF.


Figure 4: An animation showing how the parabola the surface of the water makes changes with speed, and how the vertex of that parabola need not be contained within the tank itself. This GIF was made from the video here: https://www.youtube.com/watch?v=RdRnB3jz1Yw

Now you might be wondering, since pet stores don’t sell motorized, rotating fish tanks, why might this be useful? It’s actually useful in astronomy where parabolic mirrors are used in telescopes. To build parabolic mirrors you can melt and spin glass around in a circle, letting it cool and solidify at a constant angular speed. Or you can ‘construct’ a parabolic mirror by spinning liquid mercury around. Since mercury doesn’t solidify, you have to keep spinning it for it to keep its parabolic shape, but the advantage of this is you can alter the focal length at will by simply slowing down or speeding up the rate of rotation. Such mirrors are used in what are called ‘liquid mirror telescopes’, like the one shown below.


Figure 5: A liquid mirror telescope. (Public domain image from NASA, obtained from: https://en.wikipedia.org/wiki/File:Liquid_Mirror_Telescope.jpg)

I encourage you to take a look at https://serc.carleton.edu/dmvideos/index.html and use some of their videos in your classroom in the future. Also, be sure to check out https://www.pivotinteractives.com/ and http://www.rit.edu/cos/livephoto/ for more excellent videos of various experiments. Some of the experiments, like this one, act as a good hook for a lesson; whereas others can be used to collect lab data as part of a lab writeup.

Tags: Fluids, Kinematics, Math, Motion, Pressure