Felipe Almeida, Toronto District School Board
felipe.almeida@tdsb.on.ca

As every student in an introductory physics course (like SPH3U, the grade 11 physics course in Ontario) is untrained, all their practice should be portioned appropriately in both task and problem. I have created scaffolded practice problems for the grade 11 physics course in Google Forms so students can submit their responses for immediate feedback. The forms are intended to save time and make practice/‘homework’ more meaningful and rewarding for both teachers and students. This article presents the forms used for portioned practice, a future article will present fast feedback.

Portioning Errors
Imagine, if you will, a parent doing this:



Clearly this is a bad idea, but physics teachers can make an equivalent kind of portioning error by asking students to do this:



How is this a portioning error? Unless already trained, completing the problem's full solution requires too much physics to be done at once:



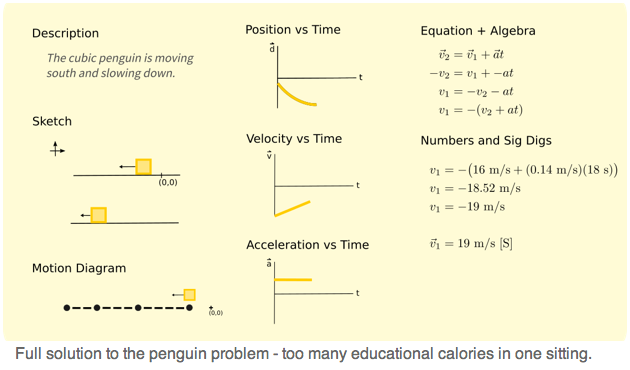
So, the responsible physics teacher chunks the problem by only asking for parts of the full solution at a time (e.g. complete sketches and motion diagrams only). But if the problem itself doesn't change, the chunking actually looks like this:



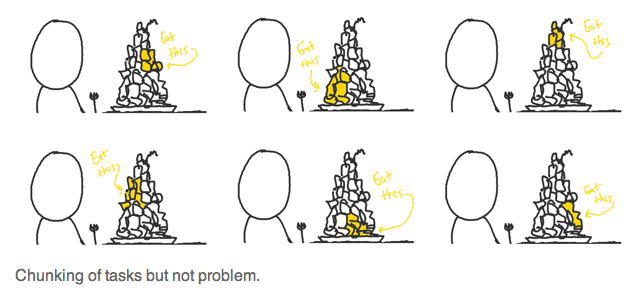
Rather than like this:



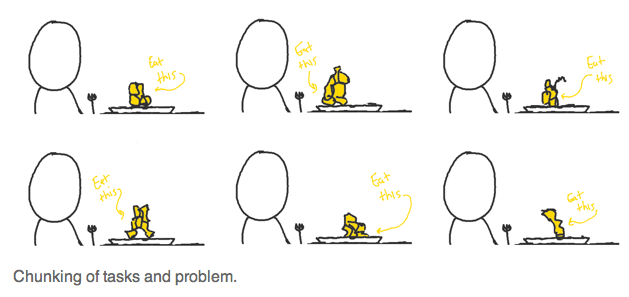Portioned Practice
As every student in an introductory physics course (like SPH3U, the grade 11 physics course in Ontario) is untrained, all their practice should be portioned appropriately in both task and problem. To that end, I created practice for several grade 11 topics as Google Forms¹, all of which can be found here. Next is a description of what the penguin problem (above) would look like in these forms, and why.

The Penguin Problem: Portioned and Fully Formed

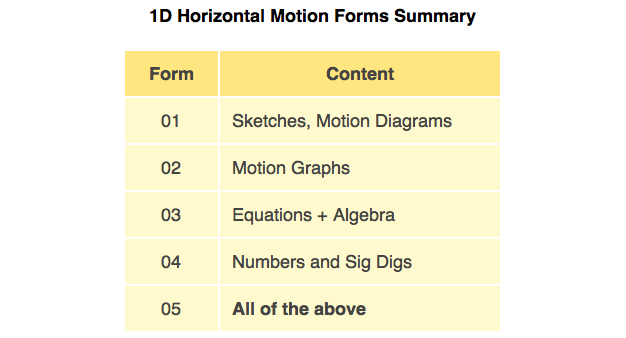
Form 01
Once students understand how to make adequate sketches and motion diagrams, they are ready for practice. But as written, the penguin problem is not yet ready for them! Let's fix that.

To begin, we recognize that the penguin problem, like many typical physics problems, comes in two parts: setup and question.



Since the question is not necessary to make sketches and motion diagrams, it can be removed.



For the same reason, so too the numbers.



There is new physics vocabulary here (e.g. ‘accelerated’ and ‘velocity’) that can be replaced with more accessible language. This allows students to make their sketches and motion diagrams (and later motion graphs) successfully without needing a total grasp of the new terms yet.



One last detail to consider: penguins have feet. If students, consciously or not, hold the 'misconception of self-acceleration', then successfully solving motion problems reinforces the misconception². Instead, a cubic penguin³ is used, and now the penguin problem is ready for Form 01.



Form 02
After an introduction to motion graphing, students can start Form 02 using the same version of the penguin problem as found in Form 01.



Form 03
With the successful completion of Forms 01 and 02, students should be confident using the motion terms previously removed and ready to see them expressed algebraically. Motion equations can then be introduced and, with the return of the question and variables for numbers, students can start practicing their algebra skills⁴.



Form 04
Finally, students are ready for the original problem⁵, numbers and all.



Students may have been intimidated and overwhelmed by this problem had they not already analyzed the motion of the penguin so thoroughly. But now, all that remains for Form 04 is for students to take their equation from Form 03 and plug in numbers, solve and report appropriately.

Form 05
We've now seen how the penguin problem would appear in Forms 01-04, which contain more than one problem each so students get lots of practice with each task (the penguin problem is not one of them — it’s used as an example). Form 05, with new problems, asks for full solutions, all at once.



The idea is that students slowly build up their capabilities through Forms 01-04 and are fully trained and ready to produce expert work on Form 05. Other motion topics and topics from and other units follow a similar structure.

Fast Feedback
Portioned practice makes it easier for students to engage with traditional physics problems without compromising their depth and complexity, but it also makes it easier for students to communicate their work with machines. While teachers can't provide immediate, on demand feedback on all the work of all their students, computers can. How computers can be used to do this will be the focus of Part II (coming soon).

Use the Forms!
If you don't want to wait for part II (though I recommend you do), you can check out the forms here (grade 11 motion, forces and energy) and get access to make copies and edit your own here.


Editor’s Note: The information in this article was presented at the OAPT Physics Hour on March 4, 2021.

---

Notes

1. As an employee of the Toronto District School Board, many of Google's products and services are automatically integrated into my workflow, so using their forms for this project (and spreadsheets, email and scripting services) was a choice made out of convenience. There are, of course, more open and independent ways to achieve the same functionality.
   
   
2. Many students believe that we apply forces on ourselves when speeding up (the same goes for other 'self-propelling' objects too: 'What makes a car speed up?' 'Wheels!' 'Engine!' 'Driver!' - the untrained never say 'ground'). Since Newton's third law and all its implications in the motion of common objects is not explored until later, delaying the use of objects with feet (or wings or fins or wheels etc.) seems the responsible thing to do.
   
   
3. What the heck is a cubic penguin? A little time should be taken to establish that a cubic penguin (like all cubic animals) is not alive, is extremely durable, and is happy to participate in the strange situations it finds itself in (maybe its life is tedious otherwise?). We wouldn't want to promote the endangerment or mistreatment of actual animals. Other than that, it's essentially cube with personality, and cubes are wonderful beginning objects to analyze the motion of because they
   
   • slide when in motion (and sliding is much simpler than rolling - now is not the time for the how-braking-causes-wheels-to-push-the-ground-forwards-/-ground-to-push-the-wheels-backwards conversation, or for worrying about rolling friction and conservation of angular momentum).
     
   • need to be pushed or pulled by some other object to speed up (which avoids reinforcing the 'misconception of self-acceleration' as described in 2.
4. Though many students are accustomed to immediately subbing numbers into equations, by not including them, algebraic errors can be separated from numeric ones. Algebra not that important to you? Skip to Form 04.
   
   
5. With 'cubic' optional (i.e. are your students ready to make their own assumptions yet?)

Tags: Pedagogy, Remote Learning, Technology