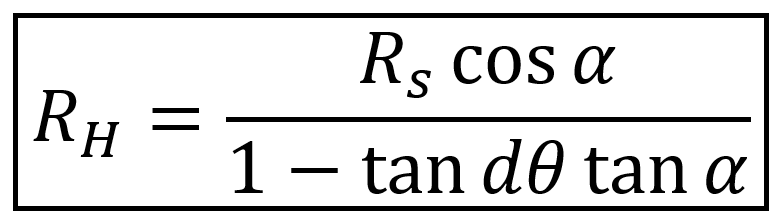Eric Haller, Secondary Long Term Occasional Teacher, Peel District School Board
eric.haller@peelsb.com

A couple of years ago I bought a bow and got into the sport of archery. To improve my accuracy at the range, I decided to invest in a laser rangefinder that could tell me the distance to my target, and its angle of elevation/depression. After using it for the first time, I discovered a third feature I was not aware of, the “Angle Intelligence™ Distance” (as it is referred to in the HALO OPTICS user’s manual). Interestingly, the rangefinder takes the angle of elevation/depression and the line-of-sight distance to the target into account, and calculates an adjusted distance to the target, as though I were instead shooting at a target across a perfectly horizontal field. Reading through the entire user’s manual, I couldn’t find any mention of what formula they used for the calculation, so I figured I would try working it out for myself.


Figure 1: A HALO OPTICS laser rangefinder, along with an excerpt from its user’s manual describing its trademarked Angle Intelligence™ Distance.

After a few hours of trying with a pen and paper, I discovered it was a lot more difficult of a problem than I had initially thought, so I turned to the internet. I eventually found the formula I was looking for; named, the “rifleman’s rule.” The rule is fairly complicated to derive, however no part of the derivation requires anything beyond a grade 12 understanding of physics or mathematics. This article will guide you through the derivation of the rifleman’s rule. As a physics teacher, you could work through it with your students, use this knowledge to help your school’s archery team, or even perhaps use it in the field yourself.

Before we derive the rifleman’s rule, we need to better understand the problem itself, and how archery works. Archers historically shot barebow, meaning their bows had no sights attached to them and they had to rely upon years of practice and instinct to hit their targets. Modern archers attach a sight to their bows, making hitting their target much easier and more reliable. A bow sight is basically just a pin attached to a bow that can be moved up and down, and left and right. They need to be calibrated after they are first attached to the bow. To do this, an archer will aim at the bullseye of a target using their uncalibrated pin and shoot a few arrows at the target. If the arrows happen to cluster to left of the target, then the archer will move their pin a tiny bit to the left to compensate. Similarly, if the arrows cluster above the bullseye, they would raise their pin. This process of “chasing the arrows” with the pin is done until the arrows consistently cluster in or around the bullseye. Once they do, the bow sight has been successfully zeroed-in.

If you calibrate your pin using a target that is 20 yards (the metric system isn’t used that frequently in archery in North America) away, but then try to shoot a target that is 30 yards away, your arrows will drop a little further over the longer distance, and you will find they will hit below the bullseye. There are numerous ways for an archer to solve this problem, one way is to use more than one pin, individually calibrating each to different distances. Here’s a picture of my bow sight, which has seven pins. I use the top pin to shoot at targets located 20 yards away, and then each successive pin is used for an additional 10 yards further.


Figure 2: A bow sight with seven fibre-optic pins, calibrated for targets 20 to 80 yards away.


Figure 3: Using the 30 yard pin to aim at a target 30 yards away, and the 80 yard pin to aim at a target 80 yards away.

It takes me about two or three days at the range to calibrate the seven different pins for seven different distances, but once complete, I can accurately shoot anything from 20 to 80 yards away. Note that if I need to hit a target that is 45 yards away, I can do so by putting the desired target in the middle of my 40 and 50 yard pins. Since the calibration process is completed on level ground, any targets I would want to hit in the future would need to be on level ground too.


Figure 4: When shooting on a horizontal field at a target 30 yards away, using the 30 yard pin, the arrow hits the centre of the target.

But what would happen if I tried to hit a target that was somewhat up a hill, but still exactly 30 yards (diagonally, or by line of sight) from myself; using the same 30 yard pin as before? It’s actually not an easy question to answer, but try pondering it before you scroll ahead.

To answer this question, I performed the experiment myself. Look at the picture below and see if it agrees with your hypothesis.


Figure 5: When shooting up a hill at a target a slant distance of 30 yards away, using the 30 yard pin, the arrow hits a little above the bullseye.

As you can see from figure 5, when shooting uphill, your arrows will typically hit a little too high. Oddly enough, if you’re shooting downhill, perhaps from a tree stand, then your arrows will again hit too high. To compensate for this, instead of using the 30 yard pin, the 20 yard pin might be more appropriate, even though the target is indeed 30 yards away! This is exactly the type of correction that the rangefinder is making for us, limited to only knowing the line-of-sight distance to the target and the angle of elevation/depression to the target. Let me try once more to rephrase the problem as clearly as possible:

A laser rangefinder is able to measure only the distance between it and the target, R_S, and the angle of elevation/depression to it, α. Given the target is R_S away, and at an angle α up or downhill, what distance pin should you use to aim at the target with? Assume the pins on bow sights are always calibrated on flat ground.

I think this would make for a good context-rich Heller & Heller type of question (a Heller, Heller & Haller problem? I should submit this problem to their website). If you aren’t familiar with the pair, Kenneth and Patricia Heller from the University of Minnesota have archived a ton of excellent, context-rich physics problems that you can access at their website. If you want your grade 12 physics students to be able to solve this difficult question, then I recommend to present it to them as a fill-in-the-blanks assignment, available here. The solutions are available here as a PDF file with extra notes written in the margins, and here as a .docx file that you could view or modify for your own use. A typical first-year university student may even be able to solve this problem without that worksheet, but with the proper scaffolding. I’ll scaffold the derivation of the rifleman’s rule for you below by breaking it into several simpler questions.

Question 1:
Fired at an angle dθ above the horizon, how far will a projectile travelling at an initial speed v_i go?


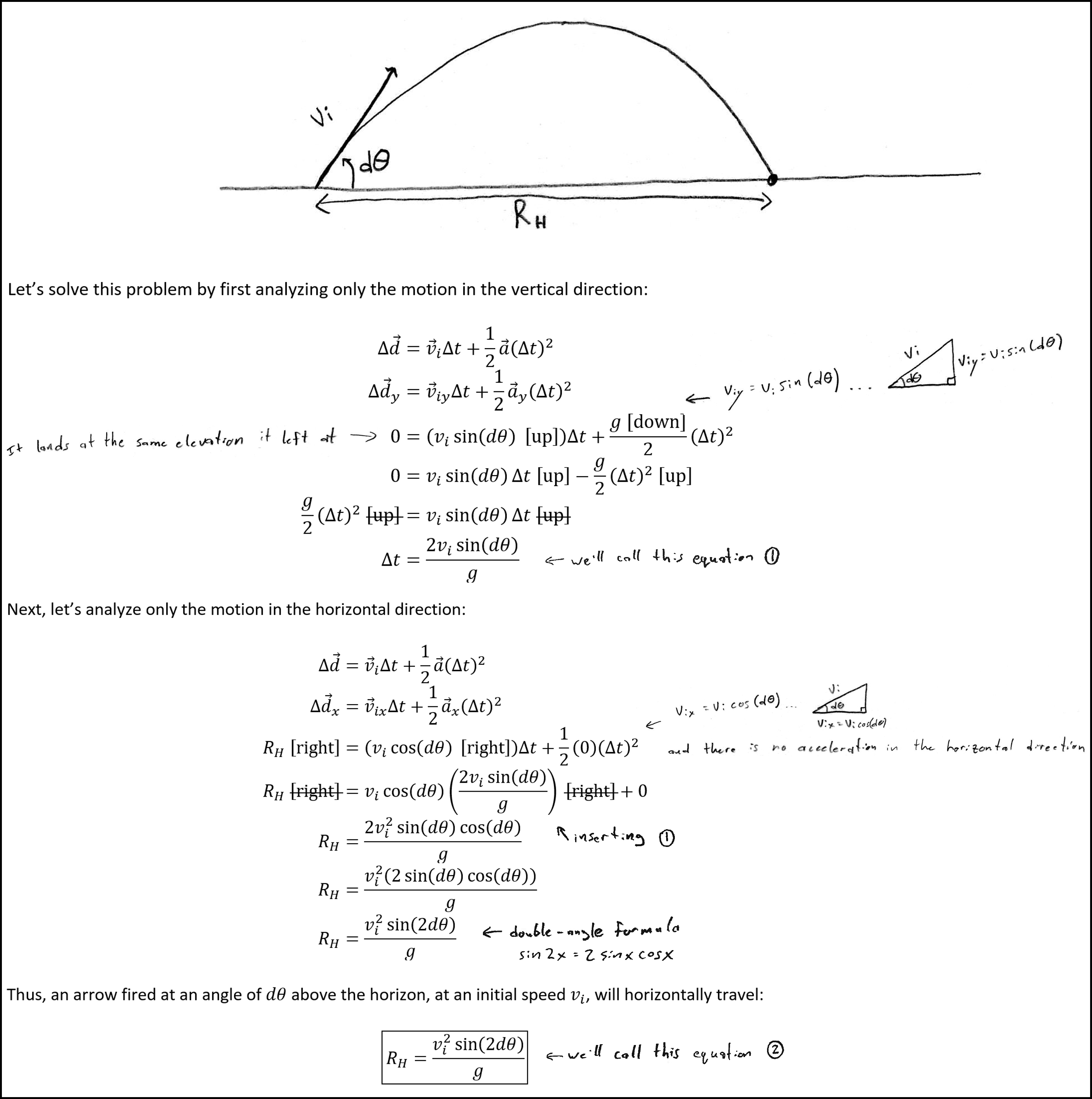Figure 6: The solution to question 1.

Question 2:
Fired at an angle dθ above a hill already at an angle α above the horizon, how far along the hill will the projectile go?


Figure 7: The solution to question 2.

Now realize that dθ corresponds to which pin we choose. Aiming with the 20 yard pin means the arrow will travel at a shallow angle above the horizon, and aiming with the 80 yard pin would result in a slightly greater (but still fairly shallow) angle above the horizon. As a reminder, the variable R_S measures the line-of-sight distance from the archer to the target and α measures the angle of the elevation/depression to the target; both of which are found using the rangefinder.

Question 3:
Rewrite your answer to question 2 (equation ④) in terms of the result from question 1 (equation ②), then assume that arrows travel in a fairly straight line and not a giant arc, meaning dθ ≈ 0. Simplify the result as much as possible.


Figure 8: The solution to question 3.

To recap, if we use a rangefinder to discover a target is a distance R_S up a hill at an angle of α, then we should aim as though we were shooting at a target that is R_S cos α away from us, across a flat field. Keen readers might notice that R_S cos α is exactly the horizontal component of the distance to the target! What an astonishingly simple result for such a complex problem. That is to say, if you want to hit a target that is up a hill, you should ignore its line-of-sight distance from you and only consider its horizontal distance. Also worth mentioning, and I’ll leave the derivation as an exercise for the reader, this same result also works for when the target is downhill, and of course the trivial case where you’re shooting across flat ground. Let’s try a practice problem to better understand this result. The user’s manual I mentioned earlier describes a scenario where a rifleman is hunting a deer; I’ll use that exact example here in order to verify that the rangefinder is indeed using the rifleman’s rule, however when presenting these kinds of scenarios to your class you may wish to change the deer to a foam target butt and the rifleman to an archer, but then you’d want to lower the distance from 366 yards down to something more realistic, like maybe 36 yards.

Question 4:
A hunter sees a deer far away and uses their laser rangefinder to determine that it is 366 yards away, at an angle of 35° below the horizon. When sighting in the target, how far away should the hunter pretend the deer is?


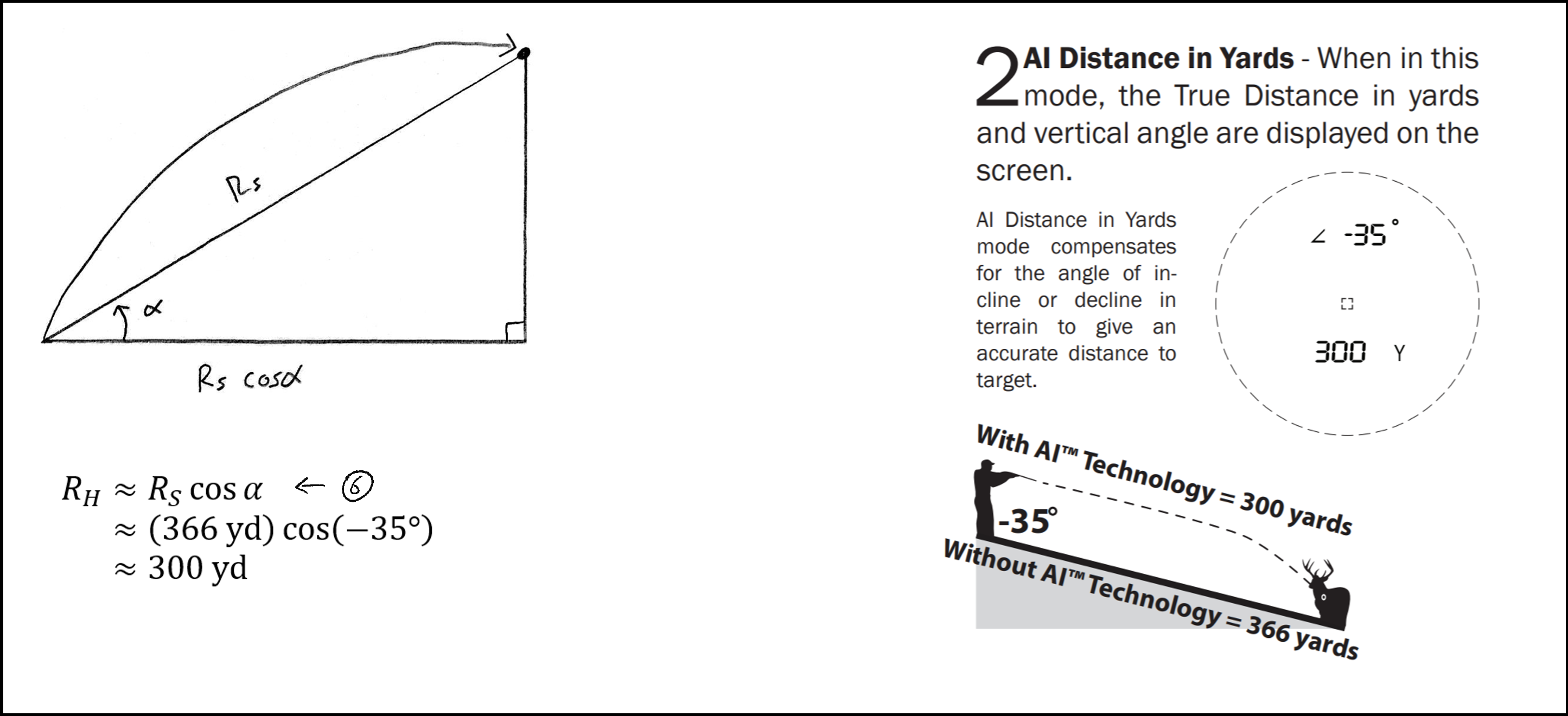Figure 9: The solution to question 4, along with the answer to the same question according to the user’s manual.

Notice our calculation and the reading from rangefinder are exactly the same! That means that the rangefinder is indeed using the rifleman’s rule, R_H = R_S cos α, to calculate its “Angle Intelligence™ Distance.” Note, however, that the rifleman’s rule is a rule of thumb, as it assumes dθ is small. Recall dθ is the angle of elevation that the arrow leaves the bow with when you’re aiming at a target across a horizontal field. For bows, and especially for firearms, this angle is usually fairly small, but caution must be used if you were to use this equation while doing something with larger launch angles, like golfing. If you need to hit a target where your launch angle isn’t small, then you would want to use the true form of the rifleman’s rule, equation ⑤ from question 3:



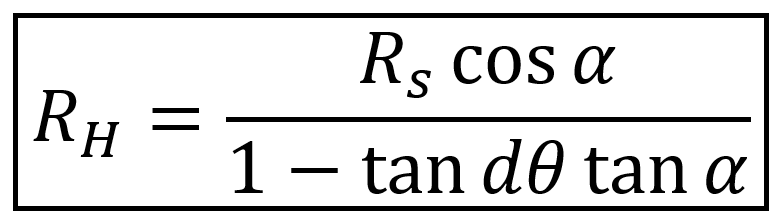
Hopefully you enjoyed learning about the rifleman’s rule. Feel free to use the worksheet and solutions documents I included earlier to work through it with your students; or better yet, use the rule in the field for yourself!

Tags: Kinematics, Projectile Motion