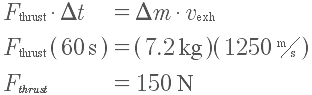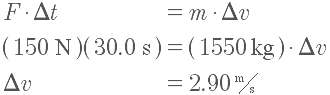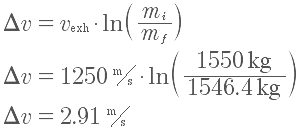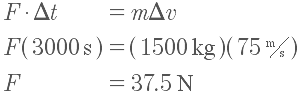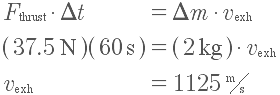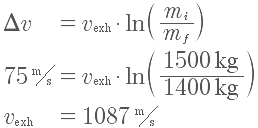John Berrigan, Teacher Oakville Trafalger H.S.
berriganj@hdsb.ca

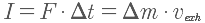
In the previous article we found the main factors that determine the thrust of a rocket engine. We rearranged the formula and determined the Impulse of the formula for rockets. With Elon Musk discussing his Mars rocket last week, http://www.spacex.com/mars, now is a good time to discuss how Impulse can be used to eventually determine the efficiency of a rocket engine.

What actually is impulse?
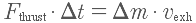
The rocket impulse formula developed in the previous article, , shows that impulse can be viewed as the product of the thrust and the time over which it is applied (the usual grade 12 approach) or as the mass of the fuel used times the speed at which it is thrown out.

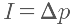
The total impulse that an engine can deliver can then be used to find the Δv of a rocket by using the impulse formula that we know. From grade 12 physics, we also know that impulse is the change in momentum or . If we use the approximation that mass is constant, this reduces to:


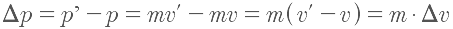
Combining this and the rocket impulse equation, we get .

Let’s apply this to a rocket problem
A 1550-kg rocket has an engine with an exhaust velocity of 1250 m/s. It uses 7.2 kg of fuel a minute. If the engine burns for 30.0 seconds, what is the velocity change of the rocket?

It is best to split the work into two parts; the rocket engine and then the change in velocity. In other words we will use the thrust equation (the cause of the change) and then the impulse equation (the result).

What do we know about each of these?

First consider the rocket engine. It uses 7.2 kg of fuel every 60 s, so:


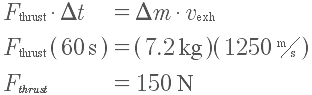
Now consider the change in velocity. The force applied is 150 N for 30 s, so:


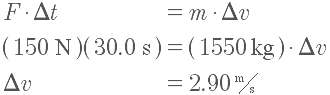
This calculation was made using a formula that assumed that the mass of the rocket was constant. However, we know that the mass is changing because fuel is flying out the back. This is an example of using an approximation — one of physics’ most powerful tools. How good is this approximation in this case? We can check it with the rocket equation .
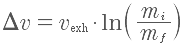
(We first explored this formula in a slightly different form here.)

The rocket used fuel at the rate of 7.2 kg/min, so in 30 s the rocket has lost 3.6 kg of mass. The final mass is 1546.4 kg. Substituting the values in the rocket equation, yields a change in velocity of

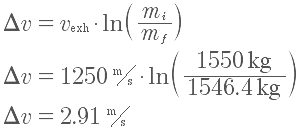
which is almost identical to our 2.90 m/s to three digits.

The first method is simpler for students because it does not require the use of logarithms. When is it better to use the “harder” method? Have them discuss this in small groups and then have each group calculate the change in velocity for a different burn time. Introduce the idea of using the average mass of the rocket rather than the starting mass. Have them use their results to explain where the approximation stops being good enough. The answer is not a simple one because it depends on how precise you need your answers to be.

Here is a Google Docs spreadsheet so you don’t have to do all the calculations each time. Once they have mastered the work using “Pen and Paper” get them to create their own spreadsheet. Getting them to use pen and paper first is essential to avoid calculations looking mathmagical.

You can mix up the question and have them solve for different variables. This gets them to think and to avoid the classic “plug and chug” questions.

Another sample problem
Here is another problem. It involves a bit more care with the units.

A 1.5 Tonne satellite needs to undergo a total delta V of 75 m/s. If 100 kg of fuel is available and the rocket uses 2 kg of fuel a minute, what must the V_exh of the engine be?

We need to solve for the thrust required first, so we start with this equation:. Fuel is burned at 2 kg/min, and we have 100 kg, which translates to 50 minutes (or 3000 seconds) of fuel to use:


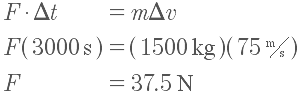
Now we know the required thrust, we can compute the exhaust velocity:


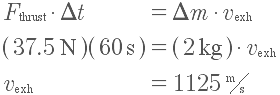
Using the rocket equation, we get:

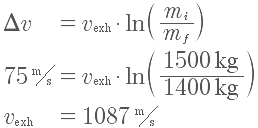
(I’ll let the reader redo this approximation using the average mass instead.)

Now that we have done some specific questions involved in impulse, this will be a good lead in to the next article which is “specific Impulse” and find out how we can define the efficiency of rocket engines.

Tags: Forces, Kinematics, Momentum, Motion